Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
495
Learners
asked the doubt

Previous Year Questions
Humans and robots can both perform a job but at different efficiencies. Fifteen humans and five robots working together take thirty days to finish the job, whereas five humans and fifteen robots working together take sixty days to finish it. How many days will fifteen humans working together (without any robot) take to finish it?
Video Explanation

Explanatory Answer
Let a Human complete ‘H’ units of work per day and a Robot complete ‘R’ units of work per day
Given,
15H + 5R = (1/30) th work per day --- (1)
5H + 15R = (1/60) th work per day --- (2)
Dividing (1) and (2) by 5 and solving,
3H + R = (1/150) and H + 3R = (1/300)
9H + 3R = 1/50
(-) H + 3R = 1/300
---------------------------
8H = 1/50 - 1/300 => 8H = 1/60
H = 1/480
Work done by 15 Humans in a day = 15/480 = 1/32
No of days required for 15 humans to complete the work = 32 days
In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is
Video Explanation

Explanatory Answer
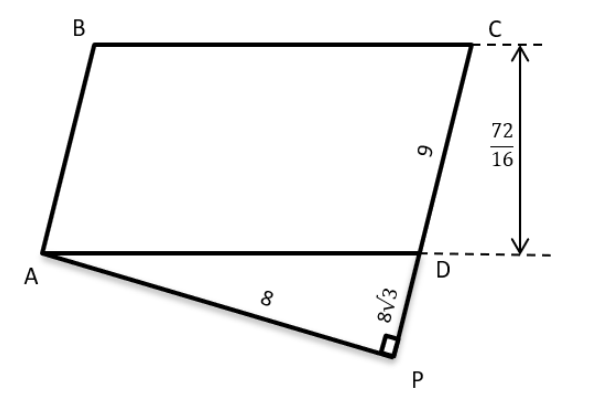
Given Area (ABCD) = 72 sq cm, CD = 9cms, AD = 16cms
Area of Parallelogram = Base × Height
CD × 16 = 72
CD = 72167216 cms
We extend CD till P such that ∠APD = 90°
So, again by applying the area formula considering CD as base
CD × AP = Area of Parallelogram ABCD
9 × AP = 72
AP = 8 cms
We have AP = 8 cms, AD = 16 cms We observe that the ratio of the sides form a 1 : √3 : 2 triangle Therefore DP = 8√3 cms Area (△APD) = 1/2 × AD × DP = 1/2 × 8 × 8√3 sq cms Area (△APD) = 32 √3 sq cms
In a circle, two parallel chords on the same side of a diameter have lengths 4 cm and 6 cm. If the distance between these chords is 1 cm, then the radius of the circle, in cm, is
Video Explanation

Explanatory Answer
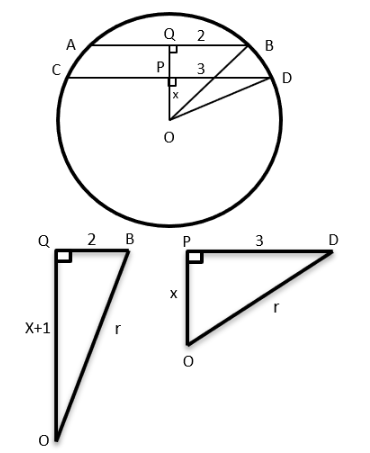
Given that Chords lie on the same side of diameter with lengths 4 cms and 6 cms
Draw a perpendicular from the origin to both the chords and mark the points of intersection as P
and Q respectively
Consider radius of circle as ‘r’ and distance OP as ‘x’
Draw lines from origin to the end of the chord and mark the points as D and B respectively
Thus, △OQB and △OPD form a right Triangle
Applying Pythagoras Theorem on both triangles,
(x+1) 2 +2 2 = r 2 ---(1)
x 2 +3 2 = r 2 ---(2)
We find that there is an increase and decrease by 1 in both equations
So, x 2 = 2 2 , x=2
r 2 = 2 2 +3 2 = 4+9 = 13
r = √13 cms
A tank is fitted with pipes, some filling it and the rest draining it. All filling pipes fill at the same rate, and all draining pipes drain at the same rate. The empty tank gets completely filled in 6 hours when 6 filling and 5 draining pipes are on, but this time becomes 60 hours when 5 filling and 6 draining pipes are on. In how many hours will the empty tank get completely filled when one draining and two filling pipes are on?
Video Explanation

Explanatory Answer
Given, Tank gets filled in 6 hours when 6 filling and 5 draining pipes are on
Let, F be the rate at which a single filling pipe fills the tanks and D be the rate at which a single
draining pipe drains the pipe
6F – 5D = 1616 th of the tank ---(1)
Also, Tank gets filled in 60 hours when 5 filling and 6 draining pipes are on
5F-6D = 160160 th of the tank ---(2)
Solving both (1) and (2) we get,
6F - 5D = 1/6
(-) 50 F - 60 D = 1/6
---------------------------
44F = 55D
F:D = 5:4
Replacing values in (1), 6F – 5D = 1/6
15D – 10D = 1/3
D = 1/15 and F = 1/12
When two filling pipes and one draining pipes are on,
2(1/6) – 1(/15) = (3/30) = 1/10 th of the tank
Therefore, they can fill the tank in 10 hours
If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
Video Explanation

Explanatory Answer
Given that out of 200 students, 105 like Pizza and 134 like Burger
In order to find the possible number of students who like only Burger, we need to find the range between the minimum and maximum possible number of students
Minimum possible number of Students who like only Burger:

For this, we must try to optimize the Venn diagram in such a way that it has maximum intersection
No of Students who like only Burger = 134 – 105= 29
Maximum possible number of Students who like only Burger:

For this, we must optimize the Venn diagram in such a way that it has minimum intersection
We know that total number of Students = 200
So, Minimum number of students who like both = 105 + 134 – 200 = 39 students
Students who like Burger = 134
Max. no of Students who like only Burger = 134 – 39 = 95
So range => 29 ≤ n ≤ 95
From the options, only (D) 93 lies within range
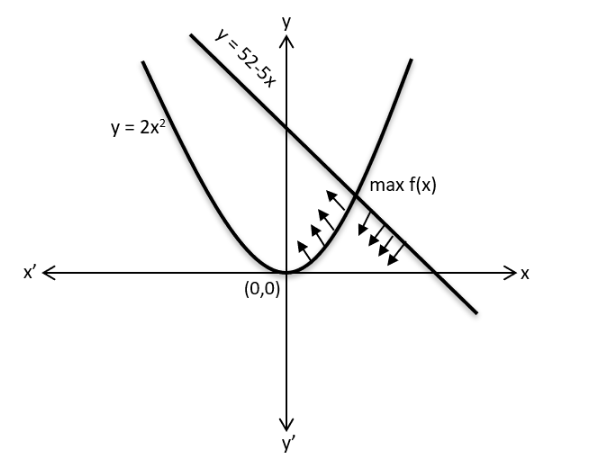
Let f(x)=min{2x2, 52 - 5x}, where x is any positive real number.Then the maximum possible value of f(x) is
Video Explanation

Explanatory Answer

In an apartment complex, the number of people aged 51 years and above is 30 and there are at most 39 people whose ages are below 51 years. The average age of all the people in the apartment complex is 38 years. What is the largest possible average age, in years, of the people whose ages are below 51 years?
Video Explanation

Explanatory Answer
Given that the Average age of all the residents in the complex = 38 years
Number of people having ages 51 and above = 30
Number of people having ages below 51 ≤ 39
Since we need to maximize the average age of people below 51 and to maintain the combined average as 38 years, we need to consider the ages of people above 51 as 51 (Any more than that would lower the other value)
Also, We need to take the Number of people having ages below as 39 (Again, for maximizing the value)

So, 13 : 38-x = 39 : 30 = 13 : 10
38 - x = 10
x = 28
Average age of people whose ages are below 51 = 28 years








