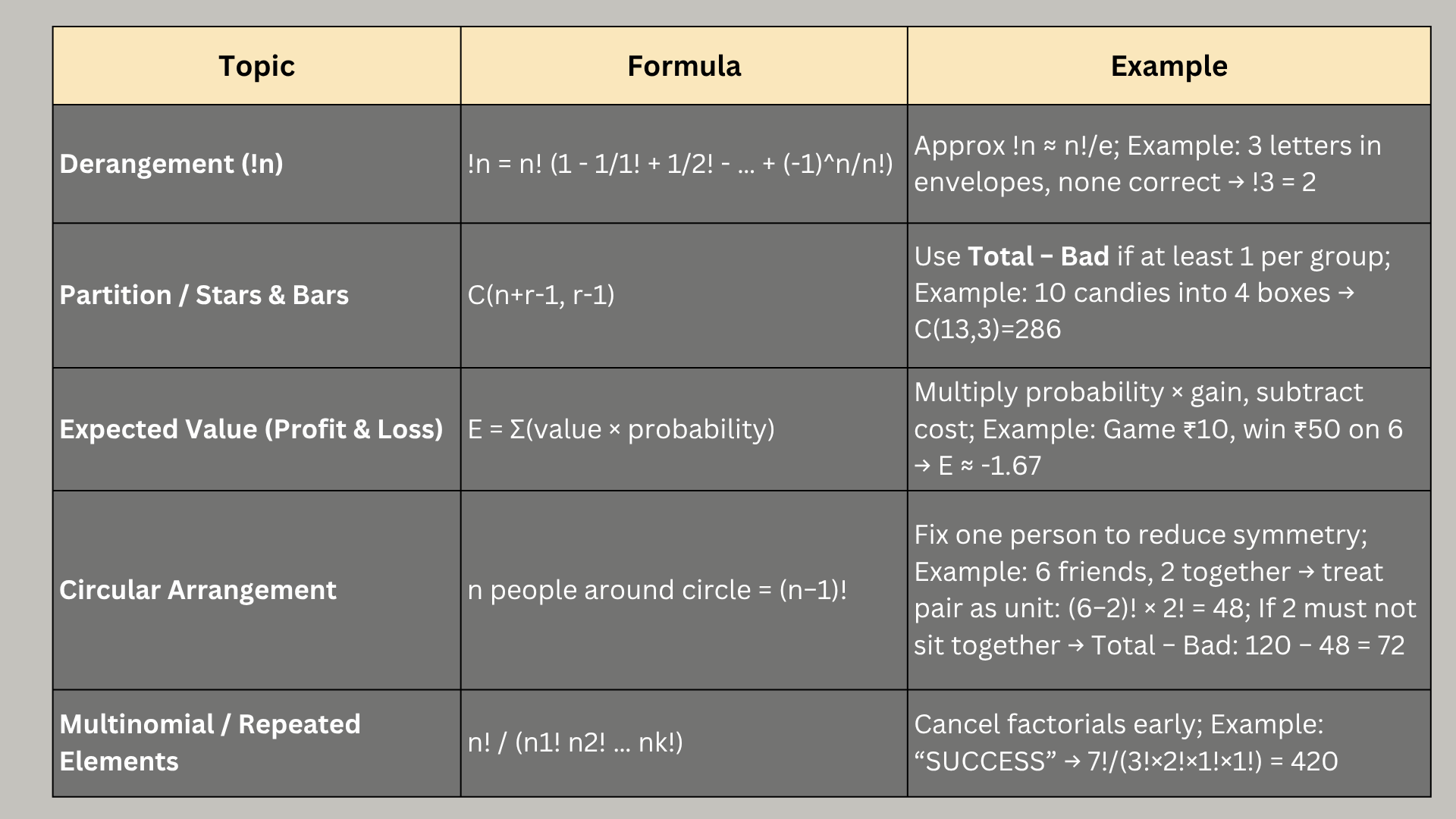
Derangements (Wrong Arrangements)

• Number of ways to arrange n objects so that none is in its original position.

• Formula: !n = n! (1−1/1! + 1/2! −1/3! +⋯+(−1)^n/n!)

Example - 3 letters A, B, C in envelopes. None should go to its original envelope.
Calculation- !3 = 3!(1 − 1+ 0.5 − 0.1667)=2

• CAT Shortcut: Memorize small n derangements (!1=0, !2=1, !3=2, !4=9) and approximate large n by !n ≈ n!/e.

"If you have 4 letters and 4 envelopes, how would you approach it mentally - formula or approximation?"

Partition / Stars & Bars Formula

• Divide n identical items among r distinct groups.

• Formula:

Number of ways = ( n + r−1)
                                    r - 1

Example - 10 identical candies into 4 boxes
Calculation - (10+4−1) = (13) = 286
                         4−1            3

• CAT Shortcut: If at least one candy per box, subtract empty cases (Total − Bad) instead of recalculating.

"If one box must have at least 3 candies, how would you adjust the calculation?"

Expected Value / Profit & Loss in Probability Games

Expected value (E) = Weighted average of outcomes:

E(X) = ∑(Value × Probability)

Example - Game costs ₹10. Roll a die: win ₹50 on a 6, nothing otherwise.
Calculation - E = (1/6×50) - 10 ≈−1.67

• CAT Shortcut: Directly multiply probability × gain − cost → avoids lengthy calculation.

"If the game cost changes to ₹5, how does expected value affect your decision?"

Circular Arrangements

• n people around a circle=(n−1)!

• Applicable when direction matters (e.g., people at a table).

Restrictions / Symmetry:

• Multiply by internal arrangements for items that must stay together.

• Divide by 2 only for objects without distinct orientation (e.g., beads on a necklace where clockwise = anticlockwise).

Example – 2 Together: 6 friends, 2 must always sit together:
Calculation - treat the pair as a single unit → now 5 units around the circle → (5−1)! = 4!
Internal arrangement of the pair → 2! Total arrangements: 4! × 2! = 48

CAT Shortcut:

• Fix one person to reduce symmetry confusion; fundamental reason why formula is (n−1)!

2 Friends Must Not Sit Together (Logic):

• Strategy: Total − Bad

  • Total arrangements: (6−1)! = 120

  • Bad arrangements (2 together): 48

  • Valid arrangements = Total − Bad = 120 − 48 = 72

"If 3 friends cannot sit together, how would you extend the Total − Bad approach?"

Multinomial Coefficient / Repeated Elements

• Arranging n objects with repeats: n!/n1!n2!…nk!

Example - “SUCCESS” → 7! / (3! × 2! × 1! × 1!) = 420 ways

• CAT Shortcut: Cancel factorials early to save time.

"If one additional letter S is added, how does the arrangement formula change?"