Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
495
Learners
asked the doubt

Previous Year Questions
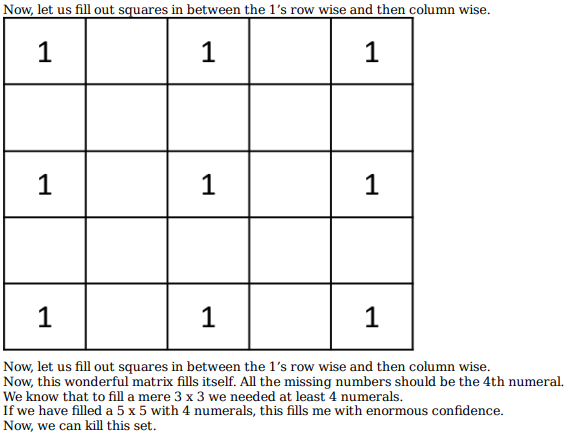
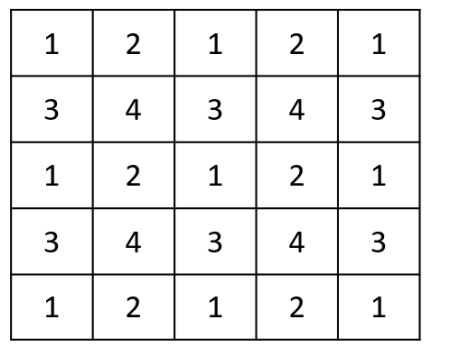
What is the minimum number of different numerals needed to fill a 5×5 square matrix? (TITA)
Video Explanation

Explanatory Answer
What is the minimum possible number of satellites serving B exclusively?
Video Explanation

Explanatory Answer

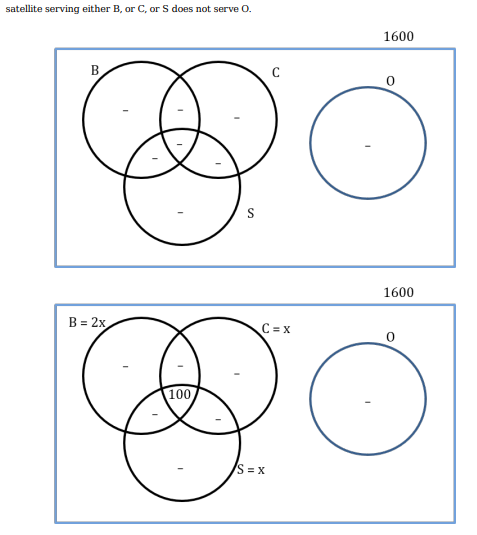
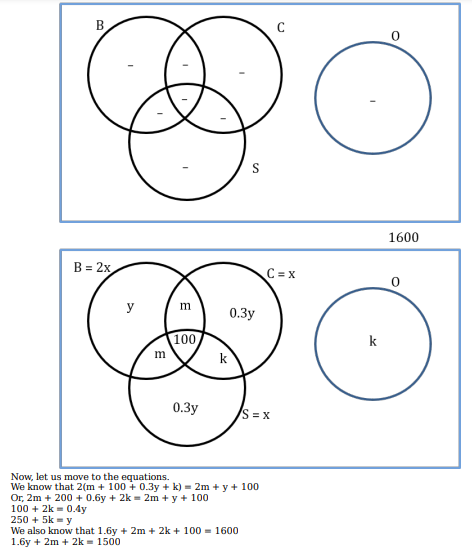
If at least 100 of the 1600 satellites were serving O, what can be said about the number of satellites serving S?
Video Explanation

Explanatory Answer



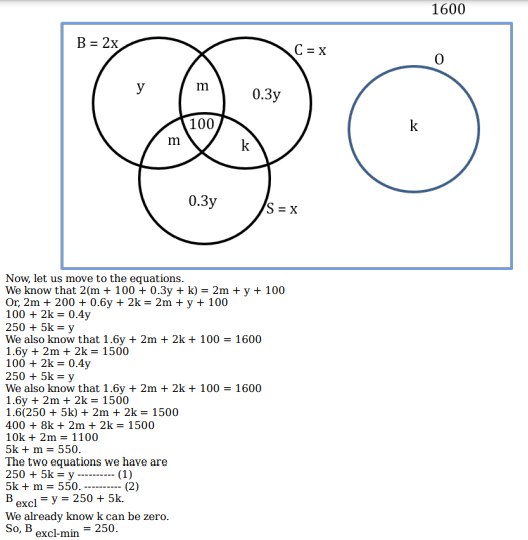
If the number of satellites serving at least two among B, C, and S is 1200, which of the following MUST be FALSE?
Video Explanation

Explanatory Answer



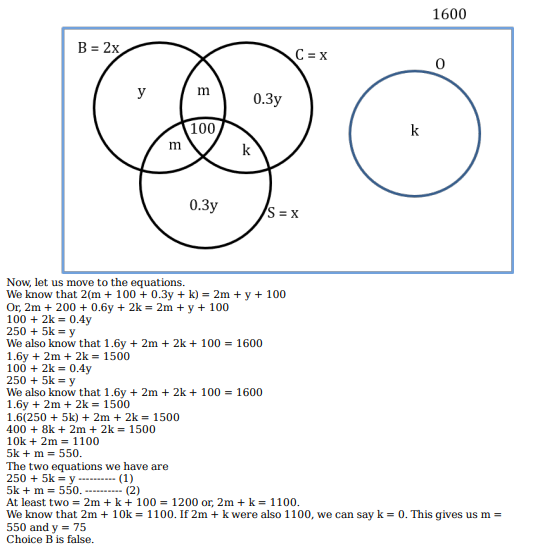
1600 satellites were sent up by a country for several purposes. The purposes are classified as broadcasting (B), communication (C), surveillance (S), and others (O). A satellite can serve multiple purposes; however a satellite serving either B, or C, or S does not serve O.
The following facts are known about the satellites:
1.The numbers of satellites serving B, C, and S (though may be not exclusively) are in the ratio 2:1:1.
2.The number of satellites serving all three of B, C, and S is 100.
3.The number of satellites exclusively serving C is the same as the number of satellites exclusively serving S. This number is 30% of the number of satellites exclusively serving B.
4.The number of satellites serving O is the same as the number of satellites serving both C and S but not B.
What best can be said about the number of satellites serving C?
Video Explanation

Explanatory Answer



What is the minimum possible number of satellites serving B exclusively?
Video Explanation

Explanatory Answer




If at least 100 of the 1600 satellites were serving O, what can be said about the number of satellites serving S?
Video Explanation

Explanatory Answer




If the number of satellites serving at least two among B, C, and S is 1200, which of the following MUST be FALSE?
Video Explanation

Explanatory Answer




What best can be said about the number of satellites serving C?
Video Explanation

Explanatory Answer




If all the candidates scored different marks in WE then what is the maximum marks that Harini could have scored in WE? (TITA)
Video Explanation

Explanatory Answer
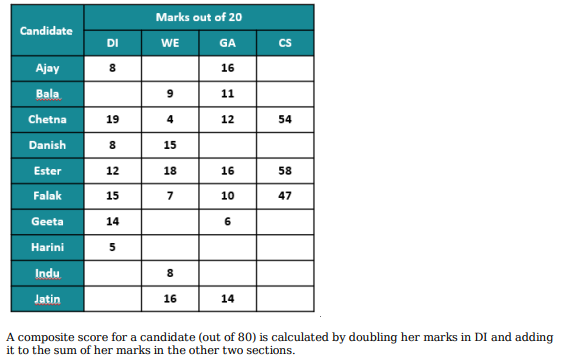
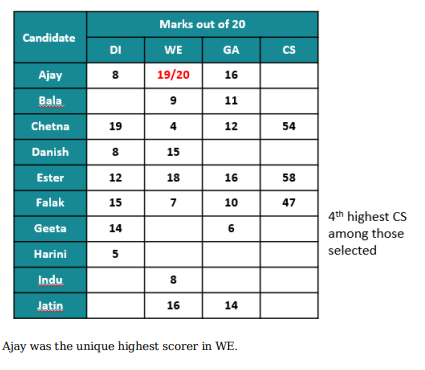
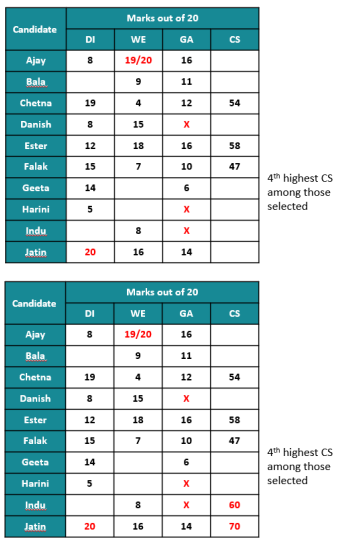
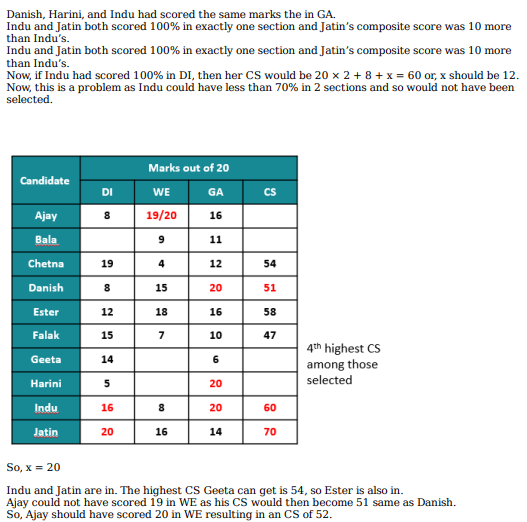
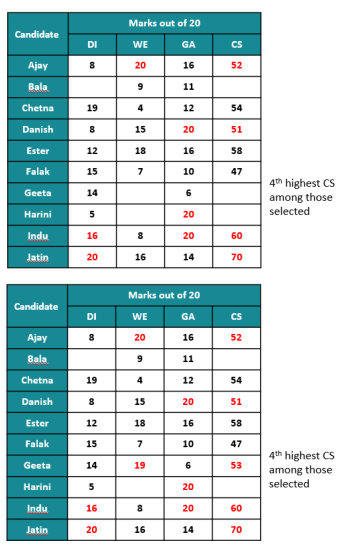


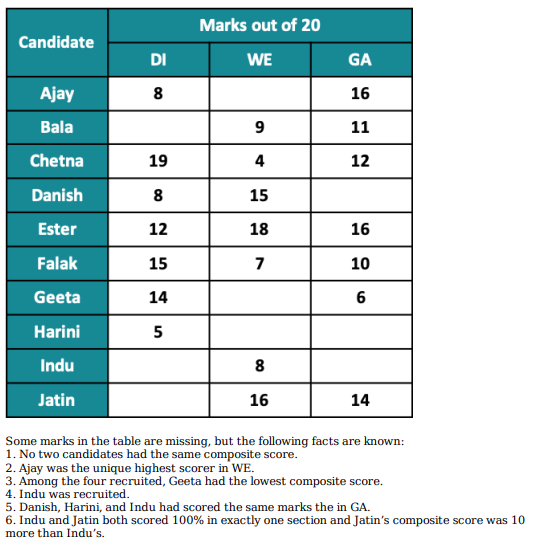
Which of the following statements MUST be true?
1.Jatin's composite score was more than that of Danish.
2. Indu scored less than Chetna in DI.
3. Jatin scored more than Indu in GA.
Video Explanation

Explanatory Answer






Which of the following statements MUST be FALSE?
Video Explanation

Explanatory Answer






If all the candidates scored different marks in WE then what is the maximum marks that Harini could have scored in WE? (TITA)
Video Explanation

Explanatory Answer






Which of the following statements MUST be true?
1.Jatin's composite score was more than that of Danish.
2. Indu scored less than Chetna in DI.
3. Jatin scored more than Indu in GA.
Video Explanation

Explanatory Answer






Which of the following statements MUST be FALSE?
Video Explanation

Explanatory Answer






What BEST can be concluded about the students who missed the Science examination?
Video Explanation

Explanatory Answer
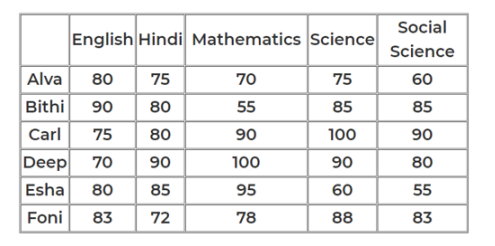
We need to check only for the ones given in the options
Alva – Hindi = 75
Average of (80+75+70)/3 = 75
Deep – Hindi = 90
Average of (100+90+80)/3 = 90
Esha – Hindi = 85
This is not the average of best 3 or 2 subjects
Hence Alva and Deep.
How many out of these six students missed exactly one examination?
Video Explanation

Explanatory Answer
Now we know that Carl only missed maths and Esha only English.
One student who missed hindi also missed science
Exams which can be missed
Alva – Hindi or Science
Bithi – Social Science and Science
Carl – Mathematics
Deep – Hindi or science
Esha – English
Foni – English and Social Science
Hence 3
For how many students can we be definite about which examinations they missed?
Video Explanation

Explanatory Answer
Exams which can be missed
Alva – Hindi or Science
Bithi – Social Science and Science
Carl – Mathematics
Deep – Hindi or science
Esha – English
Foni – English and Social Science
Either Alva or Deep can be the one who missed both Hindi and Science. Rest we are definite
Hence 4 .
In a certain board examination, students were to appear for examination in five subjects: English, Hindi, Mathematics, Science and Social Science. Due to a certain emergency situation, a few of the examinations could not be conducted for some students. Hence, some students missed one examination and some others missed two examinations. Nobody missed more than two examinations.
The board adopted the following policy for awarding marks to students. If a student appeared in all five examinations, then the marks awarded in each of the examinations were on the basis of the scores obtained by them in those examinations.
If a student missed only one examination, then the marks awarded in that examination was the average of the best three among the four scores in the examinations they appeared for.
If a student missed two examinations, then the marks awarded in each of these examinations was the average of the best two among the three scores in the examinations they appeared for.
The marks obtained by six students in the examination are given in the table below. Each of them missed either one or two examinations.
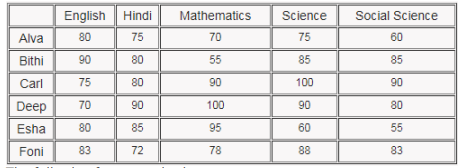
The following facts are also known.
I. Four of these students appeared in each of the English, Hindi, Science, and Social Science examinations.
II. The student who missed the Mathematics examination did not miss any other examination.
Ill. One of the students who missed the Hindi examination did not miss any other examination. The other student who missed the Hindi examination also missed the Science examination.
Who among the following did not appear for the Mathematics examination?
Video Explanation

Explanatory Answer
In this we check for the 4 options
Carl – Mathematics score = 90
This is average of best three scores 100 + 80 + 90 = 270/3 = 90
Alva – Mathematics score = 70
This cannot be the average of best three or best 2 scores
Esha – Mathematics score = 95
This is her highest score hence this is not the possible answer
Foni - – Mathematics score = 78
This cannot be the average of best three or best 2 scores
Hence Answer is Carl.
Which students did not appear for the English examination?
Video Explanation

Explanatory Answer
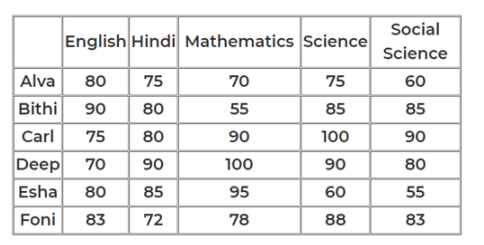
Alva and Bithi have scored the highest in English, hence they haven’t missed it.
Carl and deep have the least score in English, hence they haven’t missed it.
Esha scored 80 which is the average of (95+85+60)/3 = 80
Foni scored 83 which is the average of (88+83+78)/3 = 83
What BEST can be concluded about the students who did not appear for the Hindi examination?
Video Explanation

Explanatory Answer

We need to check only for the ones given in the options
Alva – Hindi = 75
Average of (80+75+70)/3 = 75
Deep – Hindi = 90
Average of (100+90+80)/3 = 90
Esha – Hindi = 85
This is not the average of best 3 or 2 subjects
Hence Alva and Deep.
What BEST can be concluded about the students who missed the Science examination?
Video Explanation

Explanatory Answer

We need to check only for the ones given in the options
Alva – Hindi = 75
Average of (80+75+70)/3 = 75
Deep – Hindi = 90
Average of (100+90+80)/3 = 90
Esha – Hindi = 85
This is not the average of best 3 or 2 subjects
Hence Alva and Deep.
How many out of these six students missed exactly one examination?
Video Explanation

Explanatory Answer
Now we know that Carl only missed maths and Esha only English.
One student who missed hindi also missed science
Exams which can be missed
Alva – Hindi or Science
Bithi – Social Science and Science
Carl – Mathematics
Deep – Hindi or science
Esha – English
Foni – English and Social Science
Hence 3
For how many students can we be definite about which examinations they missed?
Video Explanation

Explanatory Answer
Exams which can be missed
Alva – Hindi or Science
Bithi – Social Science and Science
Carl – Mathematics
Deep – Hindi or science
Esha – English
Foni – English and Social Science
Either Alva or Deep can be the one who missed both Hindi and Science. Rest we are definite
Hence 4 .
Who among the following did not appear for the Mathematics examination?
Video Explanation

Explanatory Answer
In this we check for the 4 options
Carl – Mathematics score = 90
This is average of best three scores 100 + 80 + 90 = 270/3 = 90
Alva – Mathematics score = 70
This cannot be the average of best three or best 2 scores
Esha – Mathematics score = 95
This is her highest score hence this is not the possible answer
Foni - – Mathematics score = 78
This cannot be the average of best three or best 2 scores
Hence Answer is Carl.
Which students did not appear for the English examination?
Video Explanation

Explanatory Answer

Alva and Bithi have scored the highest in English, hence they haven’t missed it.
Carl and deep have the least score in English, hence they haven’t missed it.
Esha scored 80 which is the average of (95+85+60)/3 = 80
Foni scored 83 which is the average of (88+83+78)/3 = 83
What BEST can be concluded about the students who did not appear for the Hindi examination?
Video Explanation

Explanatory Answer

We need to check only for the ones given in the options
Alva – Hindi = 75
Average of (80+75+70)/3 = 75
Deep – Hindi = 90
Average of (100+90+80)/3 = 90
Esha – Hindi = 85
This is not the average of best 3 or 2 subjects
Hence Alva and Deep.
Which institutes and vendors had more than one contracts in any year?
Video Explanation

Explanatory Answer
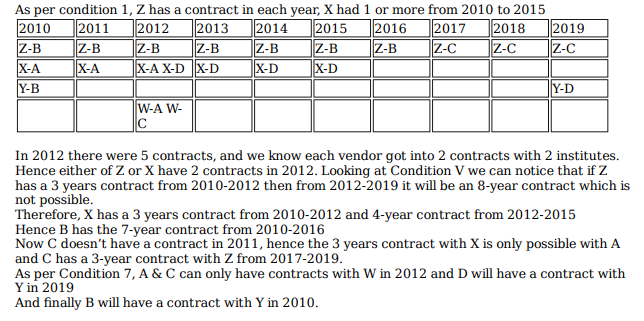
Which of the following is true?
Video Explanation

Explanatory Answer

In how many years during this period was there only one contract?
Video Explanation

Explanatory Answer

What BEST can be concluded about the number of contracts in 2010?
Video Explanation

Explanatory Answer

Which institutes had multiple contracts during the same year?
Video Explanation

Explanatory Answer

Four institutes, A, B, C, and D, had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single-year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
The following facts are also known about these contracts.
I. Vendor Z had at least one contract in every year.
II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
III. Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
IV. There were five contracts in 2012.
V. There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4-year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
VI. Institute C had one or more contracts in 2012 but did not have any contract in 2011.
VII. Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
In which of the following years were there two or more contracts?
Video Explanation

Explanatory Answer

Which of the following is true?
Video Explanation

Explanatory Answer

In how many years during this period was there only one contract?
Video Explanation

Explanatory Answer

What BEST can be concluded about the number of contracts in 2010?
Video Explanation

Explanatory Answer

Which institutes had multiple contracts during the same year?
Video Explanation

Explanatory Answer

Which institutes and vendors had more than one contracts in any year?
Video Explanation

Explanatory Answer

In which of the following years were there two or more contracts?
Video Explanation

Explanatory Answer

Who among the following is DEFINITELY an expert in mridangam but not in either tabla or ghatam?
Video Explanation

Explanatory Answer
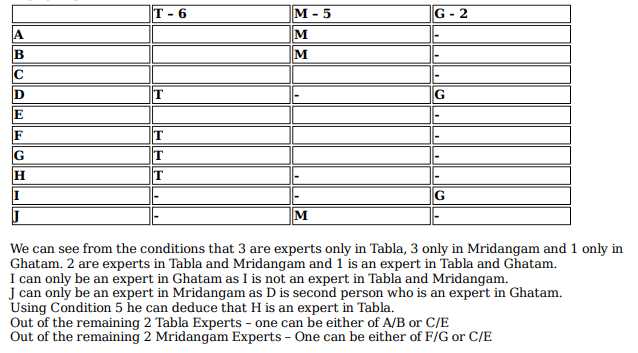
Which of the following pairs CANNOT have any musician who is an expert in both tabla and mridangam but not in ghatam?
Video Explanation

Explanatory Answer
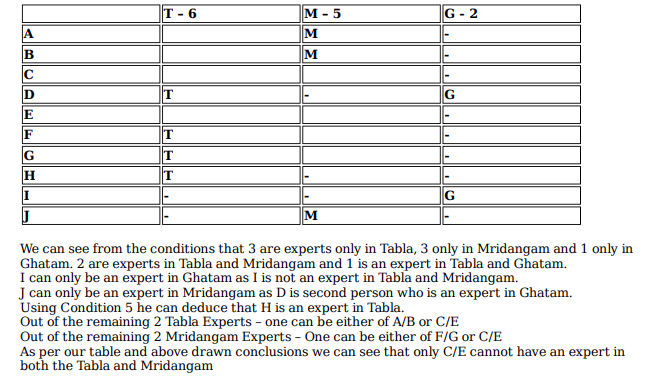
If C is an expert in mridangam and F is not, then which are the three musicians who are experts in tabla but not in either mridangam or ghatam?
Video Explanation

Explanatory Answer
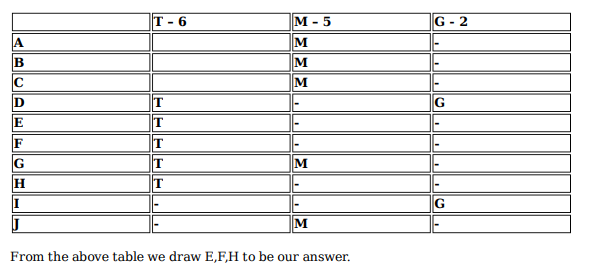
Ten musicians (A, B, C, D, E, F, G, H, I and J) are experts in at least one of the following three percussion instruments: tabla, mridangam, and ghatam. Among them, three are experts in tabla but not in mridangam or ghatam, another three are experts in mridangam but not in tabla or ghatam, and one is an expert in ghatam but not in tabla or mridangam. Further, two are experts in tabla and mridangam but not in ghatam, and one is an expert in tabla and ghatam but not in mridangam.
The following facts are known about these ten musicians.
1. Both A and B are experts in mridangam, but only one of them is also an expert in tabla.
2. D is an expert in both tabla and ghatam.
3. Both F and G are experts in tabla, but only one of them is also an expert in mridangam.
4. Neither I nor J is an expert in tabla.
5. Neither H nor I is an expert in mridangam, but only one of them is an expert in ghatam.
Who among the following is DEFINITELY an expert in tabla but not in either mridangam or ghatam?
Video Explanation

Explanatory Answer

Who among the following is DEFINITELY an expert in mridangam but not in either tabla or ghatam?
Video Explanation

Explanatory Answer

Which of the following pairs CANNOT have any musician who is an expert in both tabla and mridangam but not in ghatam?
Video Explanation

Explanatory Answer

If C is an expert in mridangam and F is not, then which are the three musicians who are experts in tabla but not in either mridangam or ghatam?
Video Explanation

Explanatory Answer

Who among the following is DEFINITELY an expert in tabla but not in either mridangam or ghatam?
Video Explanation

Explanatory Answer

Who all are NOT guiding any Economics students?
Video Explanation

Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.
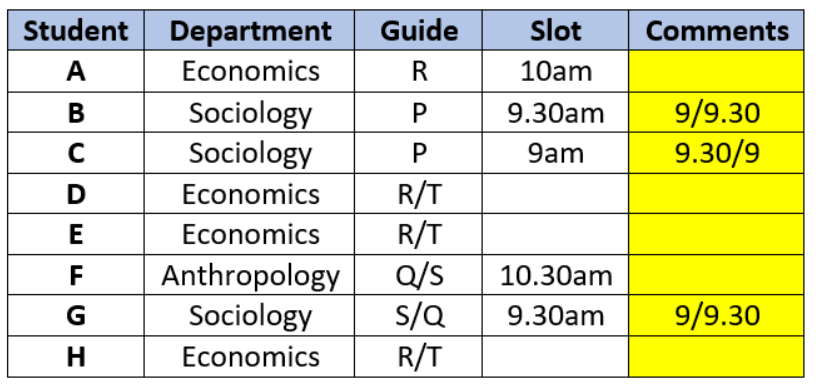
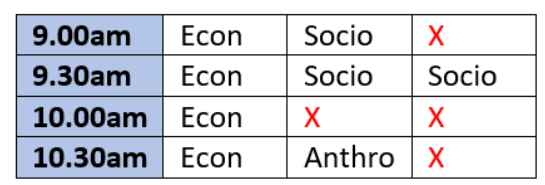
R & T are guiding Economics students while P, Q, and S are not.
Which of the following statements is necessarily true?
Video Explanation

Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.


• S may be guiding either of ‘F’ or ‘G’, so not necessarily true
• Similarly, Q may be guiding either of ‘F’ or ‘G’, so not necessarily true
• We are sure that ‘H’ is an Economics student, hence TRUE
• ‘B’ is scheduled in the second slot, hence False
If D is scheduled in a slot later than Q's, then which of the following two statement(s) is(are) true?
(i) E and H are guided by T.
(ii) G is guided by Q.
Video Explanation

Explanatory Answer
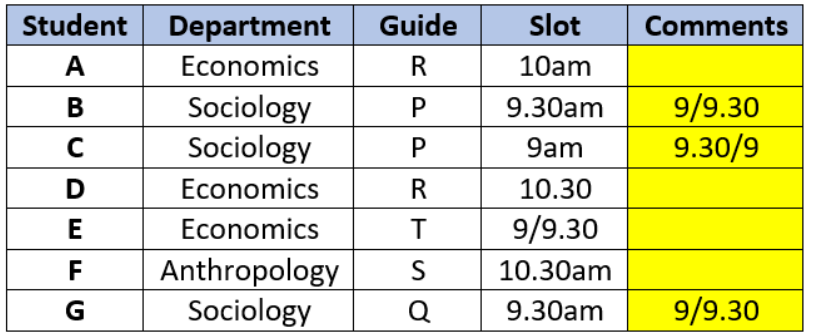
• If ‘D’ is scheduled in a slot later than Q’s, it means that Q must be in the 9.30am slot, guiding ‘G’.
Hence, S is in the 10.30am slot guiding ‘F’.
• Also, it implies that ‘D’ must be scheduled in the 10.30 slot guided by R, and ‘E’ & ‘H’ are in the
9am or 9.30am slot guided by T.
Hence, both statements are true.
If E and Q are both scheduled in the same slot, then which of the following statements BEST describes the relationship between D, H, and T?
Video Explanation

Explanatory Answer
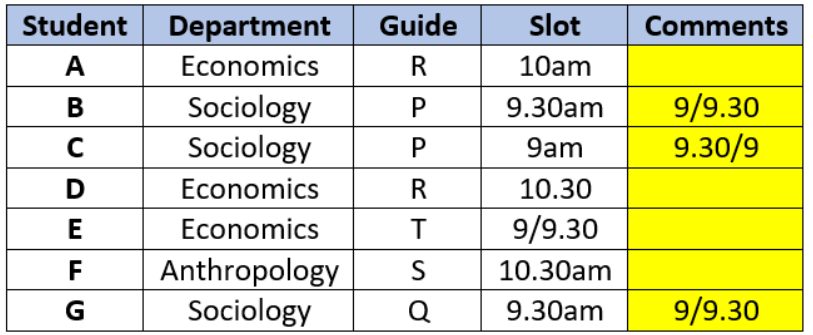
• If Q is scheduled in the 9.30am slot guiding ‘G’, ‘E’ must also be in 9.30am slot guided by T.
• If Q is scheduled in the 10.30am slot guiding ‘F’, ‘E’ must also be in 10.30am slot guided by R.
Hence, no new inferences can be gained from this information.
Since ‘A’ is guided by R, at least one of ‘D’ and ‘H’ will have to be guided by T.
If D is scheduled in the slot immediately before Q’s, then which of the following is NOT necessarily true?
Video Explanation

Explanatory Answer
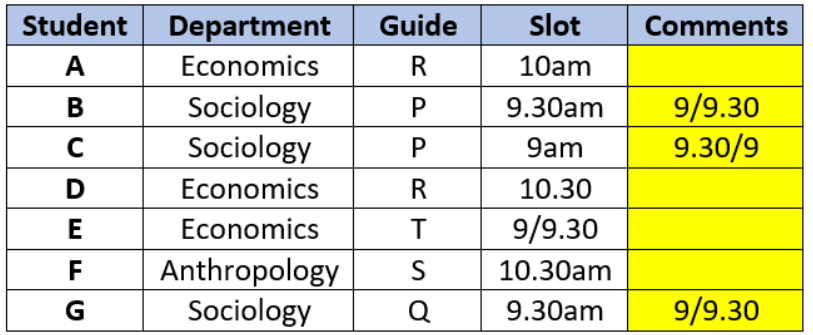
If Q is in 10.30am slot, ‘D’ must be in 10am slot. But that is not feasible as A is in the 10am slot
already and no 2 Eco students are in the same slot.
Hence, Q must be in the 9.30am slot and ‘D’ in the 9am slot guided by T. We can see from the
solution that ‘E’ may be guided by either R or T.
The Humanities department of a college is planning to organize eight seminars, one for each of the eight doctoral students - A, B, C, D, E, F, G and H. Four of them are from Economics, three from Sociology and one from Anthropology department. Each student is guided by one among P, Q, R, S and T. Two students are guided by each of P, R and T, while one student is guided by each of Q and S. Each student is guided by a guide belonging to their department.
Each seminar is to be scheduled in one of four consecutive 30-minute slots starting at 9:00 am, 9:30 am, 10:00 am and 10:30 am on the same day. More than one seminars can be scheduled in a slot, provided the guide is free. Only three rooms are available and hence at the most three seminars can be scheduled in a slot. Students who are guided by the same guide must be scheduled in consecutive slots.
The following additional facts are also known.
1. Seminars by students from Economics are scheduled in each of the four slots.
2. A’s is the only seminar that is scheduled at 10:00 am. A is guided by R.
3. F is an Anthropology student whose seminar is scheduled at 10:30 am.
4. The seminar of a Sociology student is scheduled at 9:00 am.
5. B and G are both Sociology students, whose seminars are scheduled in the same slot. The seminar of an Economics student, who is guided by T, is also scheduled in the same slot.
6. P, who is guiding both B and C, has students scheduled in the first two slots.
7. A and G are scheduled in two consecutive slots.
Which one of the following statements is true?
Video Explanation

Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.


A is clear from the solution, the first slot has 2 seminars.
Who all are NOT guiding any Economics students?
Video Explanation

Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.


R & T are guiding Economics students while P, Q, and S are not.
Which of the following statements is necessarily true?
Video Explanation

Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.


• S may be guiding either of ‘F’ or ‘G’, so not necessarily true
• Similarly, Q may be guiding either of ‘F’ or ‘G’, so not necessarily true
• We are sure that ‘H’ is an Economics student, hence TRUE
• ‘B’ is scheduled in the second slot, hence False
If D is scheduled in a slot later than Q's, then which of the following two statement(s) is(are) true?
(i) E and H are guided by T.
(ii) G is guided by Q.
Video Explanation

Explanatory Answer

• If ‘D’ is scheduled in a slot later than Q’s, it means that Q must be in the 9.30am slot, guiding ‘G’.
Hence, S is in the 10.30am slot guiding ‘F’.
• Also, it implies that ‘D’ must be scheduled in the 10.30 slot guided by R, and ‘E’ & ‘H’ are in the
9am or 9.30am slot guided by T.
Hence, both statements are true.
If E and Q are both scheduled in the same slot, then which of the following statements BEST describes the relationship between D, H, and T?
Video Explanation

Explanatory Answer

• If Q is scheduled in the 9.30am slot guiding ‘G’, ‘E’ must also be in 9.30am slot guided by T.
• If Q is scheduled in the 10.30am slot guiding ‘F’, ‘E’ must also be in 10.30am slot guided by R.
Hence, no new inferences can be gained from this information.
Since ‘A’ is guided by R, at least one of ‘D’ and ‘H’ will have to be guided by T.
If D is scheduled in the slot immediately before Q’s, then which of the following is NOT necessarily true?
Video Explanation

Explanatory Answer

If Q is in 10.30am slot, ‘D’ must be in 10am slot. But that is not feasible as A is in the 10am slot
already and no 2 Eco students are in the same slot.
Hence, Q must be in the 9.30am slot and ‘D’ in the 9am slot guided by T. We can see from the
solution that ‘E’ may be guided by either R or T.
Which one of the following statements is true?
Video Explanation

Explanatory Answer
Let’s start by consolidating all information available:
• We know we have 4 Economics, 3 Sociology, and 1 Anthropology student.
• 5 guides: P, R, and T guide 2 students each. Q and S guide one student each.
• Each student has guide belonging to same department.
• 4 slots: 9am, 9.30am, 10am, and 10.30am. Maximum 3 seminars in each slot.
Seminars guided by same person never in same slot, always in consecutive slots.
Let’s create a table and fill all further information in it:
• From (1), Economics students have seminars in all 4 slots
• From (2), 10am has only one seminar by ‘A’, hence A must be Economics student
• From (3), 10.30 has another seminar of Anthropology. ‘F’ must be the only Anthropology student.
From (4), 9am has another seminar of Sociology.
• From (5), B & G have seminars in same slot. This slot cannot be either of the last 2 slots, since we
need 2 empty slots. Hence, B & G are scheduled at either 9am or 9.30 am.
• From (6), since P is guiding B & C, C must be a Sociology student too, and B & C must have
seminars in consecutive slots. Hence, C must be 9/9.30 depending on B’s slot.
• From (7), since A’s slot is 10, G (along with B) must be scheduled at 9.30am. Consequently, C
must be scheduled at 9am.
• We know identities of 3 Sociology and 1 Anthropology student, hence remaining must be
Economics students.
• Since Q & S guide 1 student each, they must be either of Anthropology or Sociology guides, and
must guide either of F or G. Hence, R & T are Economics guides.
• Since same guides must have consecutive slots, R must have 10 and 10.30 slots while T has 9 &
9.30 slots.


A is clear from the solution, the first slot has 2 seminars.
The number of patients who were treated with medicine type D was:
Video Explanation

Explanatory Answer
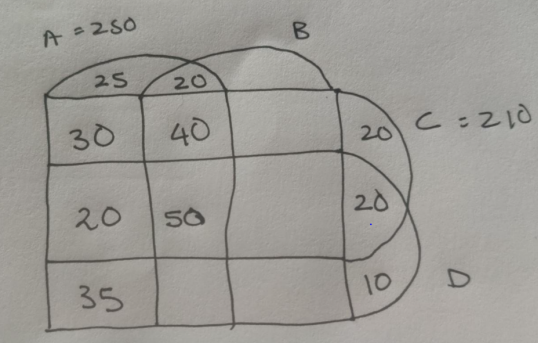
Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150
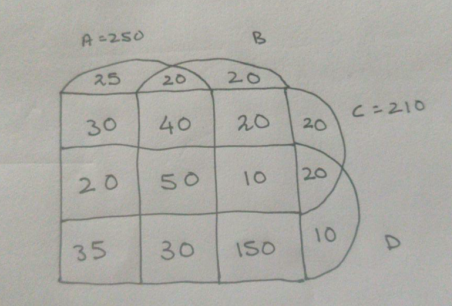
1000 patients currently suffering from a disease were selected to study the effectiveness of treatment of four types of medicines — A, B, C and D. These patients were first randomly assigned into two groups of equal size, called treatment group and control group. The patients in the control group were not treated with any of these medicines; instead they were given a dummy medicine, called placebo, containing only sugar and starch. The following information is known about the patients in the treatment group.
a. A total of 250 patients were treated with type A medicine and a total of 210 patients were treated with type C medicine.
b. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
c. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
d. 100 patients were treated with exactly three types of medicines.
e. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
f. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
How many patients were treated with medicine type B?
Video Explanation

Explanatory Answer

Using the Question we are able to fill the Venn diagram in the following manner.
Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150

The number of patients who were treated with medicine types B, C and D, but not type A was:
Video Explanation

Explanatory Answer

Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150

How many patients were treated with medicine types B and D only?
Video Explanation

Explanatory Answer

Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150

The number of patients who were treated with medicine type D was:
Video Explanation

Explanatory Answer

Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150

How many patients were treated with medicine type B?
Video Explanation

Explanatory Answer

Using the Question we are able to fill the Venn diagram in the following manner.
Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150

The number of patients who were treated with medicine types B, C and D, but not type A was:
Video Explanation

Explanatory Answer

Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150

How many patients were treated with medicine types B and D only?
Video Explanation

Explanatory Answer

Using Condition F, 75 patients were given only 1 medicine
Hence only B = 75 -25-20-10 = 20
And Medicine given to A, B, D but not C =
250-25-20-30-40-20-50-35 = 30
Exactly 100 people had taken 3 medicines hence Medicine given to B, C, D but not A =
100-40-20-30 = 10
And Since C has a total of 210 patients, hence Only B and C =
210-20-20-30-40-20-50-10 = 20
Total patients is 500
Only B and D = 500 – (250+20+20+10+20+20+10) = 150

For all the four constituencies taken together, what was the approximate number of votes polled by all the candidates who lost their security deposit expressed as a percentage of the total valid votes from these four constituencies?
Video Explanation

Explanatory Answer
Total number of valid votes in 4 constituencies = 5,00,000 + 3,25,000 + 6,00,030 + 1,75,000
= 16,00,030
We can consolidate the data about the candidates who lost security in the below table:

Therefore, total number of votes polled by candidates who lost their security deposit:
45,000 + 2,76,250 + 0 + 61,250 = 3,82,500
% = (3,82,500/16,00, 030)* 100 = 23.9%
In an election several candidates contested for a constituency. In any constituency, the winning candidate was the one who polled the highest number of votes, the first runner up was the one who polled the second highest number of votes, the second runner up was the one who polled the third highest number of votes, and so on. There were no ties (in terms of number of votes polled by the candidates) in any of the constituencies in this election.
In an electoral system, a security deposit is the sum of money that a candidate is required to pay to the election commission before he or she is permitted to contest. Only the defeated candidates (i.e., one who is not the winning candidate) who fail to secure more than one sixth of the valid votes polled in the constituency, lose their security deposits.
The following table provides some incomplete information about votes polled in four constituencies: A, B, C and D, in this election.
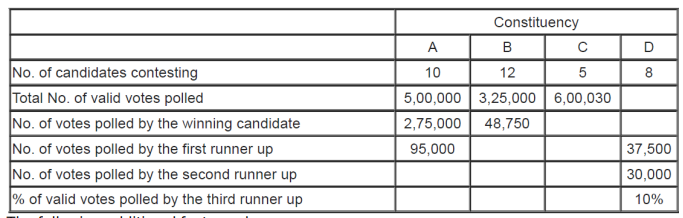
The following additional facts are known:
1. The first runner up polled 10,000 more votes than the second runner up in constituency A. 2. None of the candidates who contested in constituency C lost their security deposit. The difference in votes polled by any pair of candidates in this constituency was at least 10,000.
3. The winning candidate in constituency D polled 5% of valid votes more than that of the first runner up. All the candidates who lost their security deposits while contesting for this constituency, put together, polled 35% of the valid votes.
What is the percentage of votes polled in total by all the candidates who lost their security deposits while contesting for constituency A?
Video Explanation

Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .
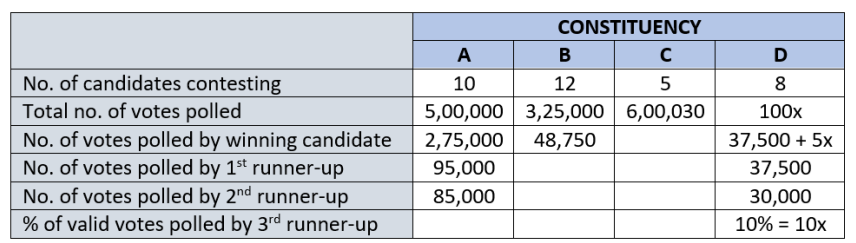
Total votes polled in A = 5,00,000
Total votes polled by top 3 candidates = 2,75,000 + 95,000 + 85,000 = 4,55,000
Votes polled by bottom 7 candidates = 5,00,000 – 4,55,000 = 45,000
We can see that 45,000 is clearly less than 1/6 th of 5,00,000 (83,333) . Hence, all the bottom 7
candidates lost their deposit.
Total % votes polled by them = \(({45000 \over {500000}})*100\) = 9%
How many candidates who contested in constituency B lost their security deposit?
Video Explanation

Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .

Total votes polled in B = 3,25,000
1/6 th of 325000 = 54166.66 ̴ 54167
We can see that the winning candidate also secured less than 1/6 th of the total valid votes.
Hence, the rest 11 candidates must have secured lesser votes than that.
Hence, 11 candidates lost their security deposit in B.
What BEST can be concluded about the number of votes polled by the winning candidate in constituency C?
Video Explanation

Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .

Total no. of votes polled in C = 6,00,030
Total no. of candidates = 5
We know that everyone polled more than 1,00,005 votes in C, and minimum diff between any 2 is
10,000.
Hence, minimum votes polled by bottom 4 :
( 1,00,006 ) + ( 1,00, 006 + 10 000) + (1,00,006 + 2*10000) + (1,00,006 + 3*10000)
= 4*1,00,006 + 60,000 = 4,60,024 votes
Maximum votes polled by winning candidate = 6,00,030 – 4,60,024 = 1,40,006
Minimum votes polled by 1 st runner-up = 1,00,006 + 30,000 = 1,30,006
Diff between the two is 10,000. Hence, we can conclude that winner polled exactly 1,40,006
votes.
What was the number of valid votes polled in constituency D?
Video Explanation

Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .

Total votes polled in D = 100x
Votes secured by top 4 = 37,500 + 5x + 37,500 + 30,000 + 10x = 1,05,000 + 15x
We can also see that the 3 rd runner-up secured less than 1/6 th (10%) votes and hence lost
security deposit. So, minimum 5 and maximum 7 candidates lost security deposit.
We can have 3 cases here:
CASE I: 7 candidates (all except winner) lost security deposit. In this case, top candidate will
have remining 65% votes.
37,500 + 5x = 65x
60x = 37,500
x = 625
Total votes polled = 100x = 62 , 500
1/6 th of 62,500 = 10,417
Votes secured by 1 st runner-up = 37,500 > 10,417
1 st runner up couldn’t have lost deposit. Hence, this case is not feasible.
CASE II: 6 candidates (all except winner & 1 st runner-up) lost security deposit. In this case, top 2
candidates will have remining 65% votes.
37,500 + 5x + 37,500 = 65x
75,000 = 60x
x = 1250
Total votes polled = 100x = 1,25,000
1/6 th of 1,25,000 = 20,833
Once again, 1 st runner-up secured more than 1/6 th votes and couldn’t have lost deposit. This
case is also not feasible.
CASE III: 5 candidates (all except winner, 1 st runner-up & 2 nd runner-up) lost security deposit.
In this case, top 3 candidates will have remining 65% votes.
75,000 + 5x + 30,000 = 65x
60x = 1,05,000
x = 17 50
Total votes polled = 100x = 1,75,000
1/6 th of 1,75,000 = 29,167
Votes secured by 3 rd runner-up = 10x = 10,500 < 29,167
Hence, this is the only feasible case.
Therefore, total number of valid votes polled in D is 1,75,000.
The winning margin of a constituency is defined as the difference of votes polled by the winner and that of the first runner up. Which of the following CANNOT be the list of constituencies, in increasing order of winning margin?
Video Explanation

Explanatory Answer
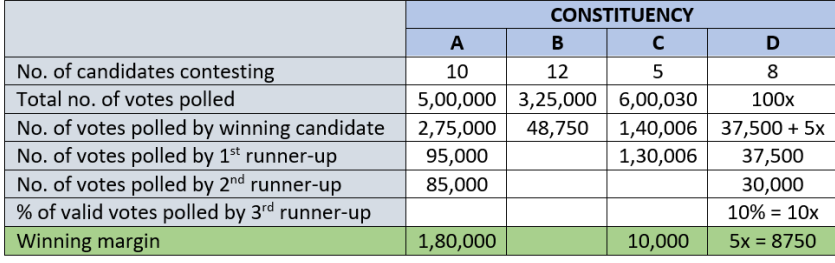
The confirmed order we know is D < C < A. ‘B’ could be anywhere in between except more than
A.
Hence, B < C < D < A is not possible as we know that margin of C is greater than that of D.
For all the four constituencies taken together, what was the approximate number of votes polled by all the candidates who lost their security deposit expressed as a percentage of the total valid votes from these four constituencies?
Video Explanation

Explanatory Answer
Total number of valid votes in 4 constituencies = 5,00,000 + 3,25,000 + 6,00,030 + 1,75,000
= 16,00,030
We can consolidate the data about the candidates who lost security in the below table:

Therefore, total number of votes polled by candidates who lost their security deposit:
45,000 + 2,76,250 + 0 + 61,250 = 3,82,500
% = (3,82,500/16,00, 030)* 100 = 23.9%
What is the percentage of votes polled in total by all the candidates who lost their security deposits while contesting for constituency A?
Video Explanation

Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .

Total votes polled in A = 5,00,000
Total votes polled by top 3 candidates = 2,75,000 + 95,000 + 85,000 = 4,55,000
Votes polled by bottom 7 candidates = 5,00,000 – 4,55,000 = 45,000
We can see that 45,000 is clearly less than 1/6 th of 5,00,000 (83,333) . Hence, all the bottom 7
candidates lost their deposit.
Total % votes polled by them = \(({45000 \over {500000}})*100\) = 9%
How many candidates who contested in constituency B lost their security deposit?
Video Explanation

Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .

Total votes polled in B = 3,25,000
1/6 th of 325000 = 54166.66 ̴ 54167
We can see that the winning candidate also secured less than 1/6 th of the total valid votes.
Hence, the rest 11 candidates must have secured lesser votes than that.
Hence, 11 candidates lost their security deposit in B.
What BEST can be concluded about the number of votes polled by the winning candidate in constituency C?
Video Explanation

Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .

Total no. of votes polled in C = 6,00,030
Total no. of candidates = 5
We know that everyone polled more than 1,00,005 votes in C, and minimum diff between any 2 is
10,000.
Hence, minimum votes polled by bottom 4 :
( 1,00,006 ) + ( 1,00, 006 + 10 000) + (1,00,006 + 2*10000) + (1,00,006 + 3*10000)
= 4*1,00,006 + 60,000 = 4,60,024 votes
Maximum votes polled by winning candidate = 6,00,030 – 4,60,024 = 1,40,006
Minimum votes polled by 1 st runner-up = 1,00,006 + 30,000 = 1,30,006
Diff between the two is 10,000. Hence, we can conclude that winner polled exactly 1,40,006
votes.
What was the number of valid votes polled in constituency D?
Video Explanation

Explanatory Answer
We know that candidates who failed to secure more 1/6 th of total valid votes lose their
security deposit.
Let us put the information we have in a table:
• From (1), we know that the 2 nd runner-up in A polled 95000-10000 = 85000 votes
• From (2), we know that everyone in C secured more than (1/ 6)* 600030 = 100005 votes . Also,
the minimum difference between any 2 candidates’ votes was 10,000.
• From (3), let’s assume the total no. of votes polled in D was 100x. Then votes polled by winner =
37,500 + 5x.
Also, we know that candidates who lost their deposit in D together polled 35% votes .

Total votes polled in D = 100x
Votes secured by top 4 = 37,500 + 5x + 37,500 + 30,000 + 10x = 1,05,000 + 15x
We can also see that the 3 rd runner-up secured less than 1/6 th (10%) votes and hence lost
security deposit. So, minimum 5 and maximum 7 candidates lost security deposit.
We can have 3 cases here:
CASE I: 7 candidates (all except winner) lost security deposit. In this case, top candidate will
have remining 65% votes.
37,500 + 5x = 65x
60x = 37,500
x = 625
Total votes polled = 100x = 62 , 500
1/6 th of 62,500 = 10,417
Votes secured by 1 st runner-up = 37,500 > 10,417
1 st runner up couldn’t have lost deposit. Hence, this case is not feasible.
CASE II: 6 candidates (all except winner & 1 st runner-up) lost security deposit. In this case, top 2
candidates will have remining 65% votes.
37,500 + 5x + 37,500 = 65x
75,000 = 60x
x = 1250
Total votes polled = 100x = 1,25,000
1/6 th of 1,25,000 = 20,833
Once again, 1 st runner-up secured more than 1/6 th votes and couldn’t have lost deposit. This
case is also not feasible.
CASE III: 5 candidates (all except winner, 1 st runner-up & 2 nd runner-up) lost security deposit.
In this case, top 3 candidates will have remining 65% votes.
75,000 + 5x + 30,000 = 65x
60x = 1,05,000
x = 17 50
Total votes polled = 100x = 1,75,000
1/6 th of 1,75,000 = 29,167
Votes secured by 3 rd runner-up = 10x = 10,500 < 29,167
Hence, this is the only feasible case.
Therefore, total number of valid votes polled in D is 1,75,000.
The winning margin of a constituency is defined as the difference of votes polled by the winner and that of the first runner up. Which of the following CANNOT be the list of constituencies, in increasing order of winning margin?
Video Explanation

Explanatory Answer

The confirmed order we know is D < C < A. ‘B’ could be anywhere in between except more than
A.
Hence, B < C < D < A is not possible as we know that margin of C is greater than that of D.
What was the increase in sales amount, in Crore Rupees, in the Apparel department of Mumbai from 2018 to 2019?
Video Explanation

Explanatory Answer

From (4),
Increase in Electronics sales from 2018 to 2019:
(98+102+70+100) – (78+82+90+80) = 4 0 = Increase in Apparels sales from 2018 to 2019
• From (5),
Total sales in Home Décor in 2019 = 100+72+80+54 = 306
Hence, Total sales in Home Décor in 2018 = 306 – 70 = 236
From (6), we know sales of Home Décor in 2018 of Delhi and Bangalore.
80 + Z + 60 + Z = 236
2Z = 96
Z = 48
• From (7), we know that
Y – X = B – Y
2Y = B + X
B = 2Y – X -----------( i )
Also,
A – Y = 54 – X ---------(ii)
• F rom (8), we know that Y , 54, and B are in A.P.
54 – Y = B – 54
B = 108 – Y ----------(iii)
Therefore, from ( i ) we get
108 – Y = 2Y – X
X = 3Y – 108 ------------(iv)
And (ii) becomes:
A – Y = 54 – (3Y – 108)
A = 54 – 3Y + 108 + Y
A = 162 – 2Y ----------(v)
• From (4), we knew that
( Y +A+B+54) – (X+ Y+Y +X) = 4 0
Substituting values from (iii), (iv), and (v), we get:
(Y+162-2Y+108-Y+54) – (3Y-108 +Y+Y+3Y-108) = 40
324 – 2Y – 8Y + 216 = 40
10Y = 500
Y = 50
Therefore, we get values of A, B, and X by substituting values of Y.
A = 162 – 2Y = 162 – 100
A = 62
B = 108 – y = 108 – 50
B = 58
X = 3Y – 108 = 150 – 108
X = 42
Therefore, our final table looks like this:

Mumbai’s sales in Apparel department increased by 12 crores (62cr – 50cr)









