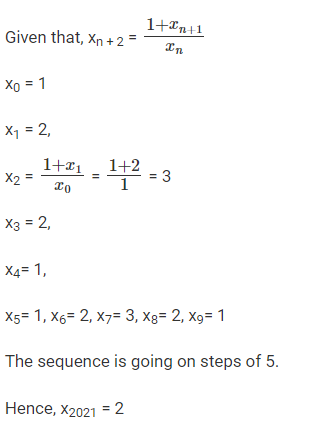Live Updates
• CATKing has launched new chat bot.
• New video on Logs has been released.
495
Learners
asked the doubt
Previous Year Questions
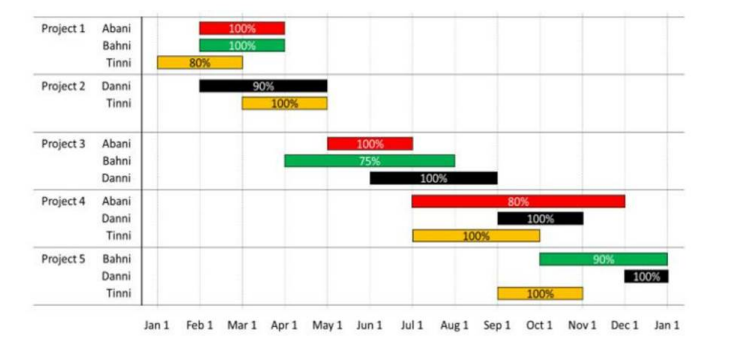
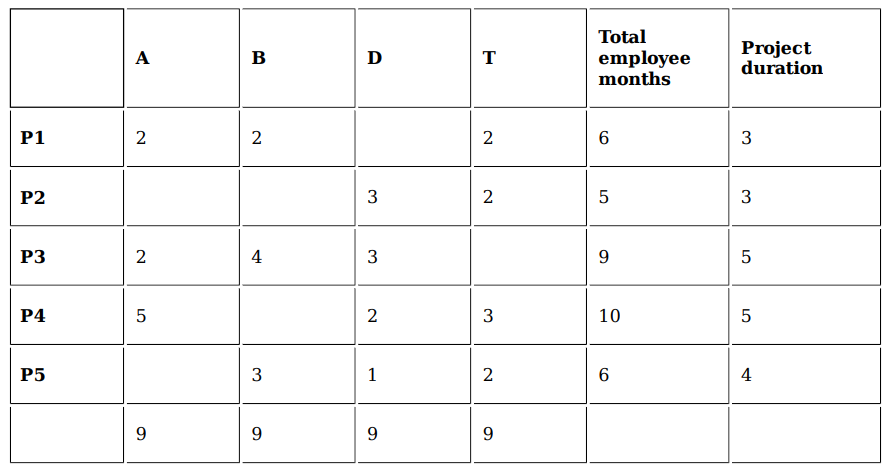
The figure above shows the schedule of four employees – Abani, Bahni, Danni and Tinni – whom Dhoni supervised in 2020. Altogether there were five projects which started and concluded in 2020 in which they were involved. For each of these projects and for each employee, the starting day was at the beginning of a month and the concluding day was the end of a month, and these are indicated by the left and right end points of the corresponding horizontal bars. The number within each bar indicates the percentage of assigned work completed by the employee for that project, as assessed by Dhoni.
For each employee, his/her total project-month (in 2020) is the sum of the number of months (s)he worked across the five project, while his/her annual completion index is the weightage average of the completion percentage assigned from the different projects, with the weights being the corresponding number of months (s)he worked in these projects. For each project, the total employee-month is the sum of the number of months four employees worked in this project, while its completion index is the weightage average of the completion percentage assigned for the employees who worked in this project, with the weights being the corresponding number of months they worked in this project.
Which of the following statements is/are true?
I: The total project-month was the same for the four employees.
II: The total employee-month was the same for the five projects.
Video Explanation
Explanatory Answer
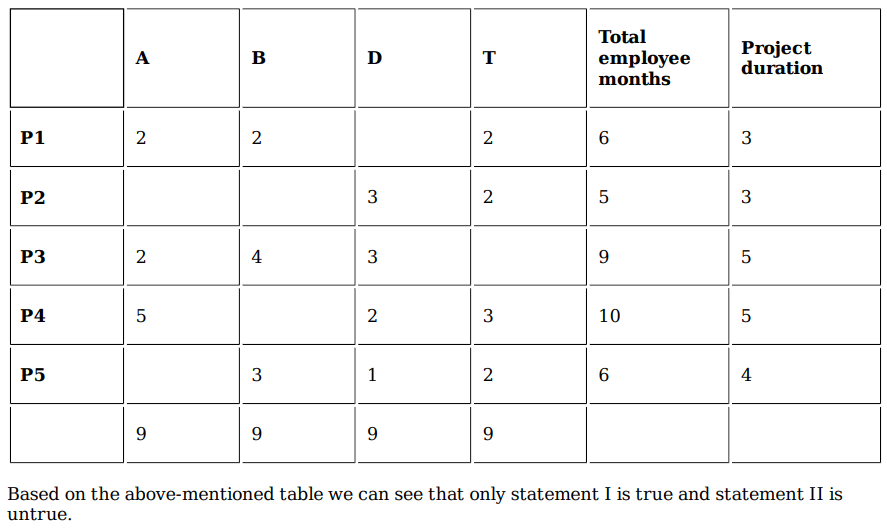
Which employees did not work in multiple projects for any of the months in 2020?
Video Explanation
Explanatory Answer
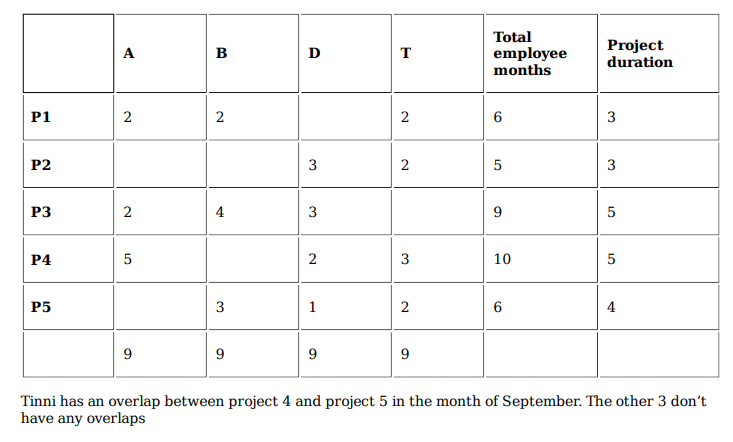
The project duration, measured in terms of the number of months, is the time during which at least one employee worked in the project. Which of the following pairs of the projects had the same duration?
Video Explanation
Explanatory Answer
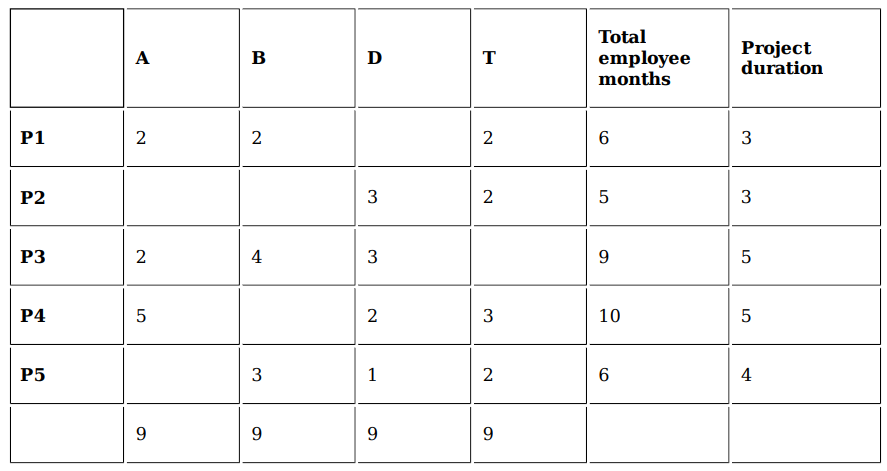
Project 1 & 2 as well as Project 3 & 4 have the same number of months but in the options we only
have Project 3 & 4.
The list of employees in decreasing order of annual completion index is:
Video Explanation
Explanatory Answer
Which of the following statements is/are true?
I: The total project-month was the same for the four employees.
II: The total employee-month was the same for the five projects.
Video Explanation
Explanatory Answer
Which employees did not work in multiple projects for any of the months in 2020?
Video Explanation
Explanatory Answer
The project duration, measured in terms of the number of months, is the time during which at least one employee worked in the project. Which of the following pairs of the projects had the same duration?
Video Explanation
Explanatory Answer
Project 1 & 2 as well as Project 3 & 4 have the same number of months but in the options we only
have Project 3 & 4.
The list of employees in decreasing order of annual completion index is:
Video Explanation
Explanatory Answer
What was the final score (in m) of the silver-medalist?
Video Explanation
Explanatory Answer
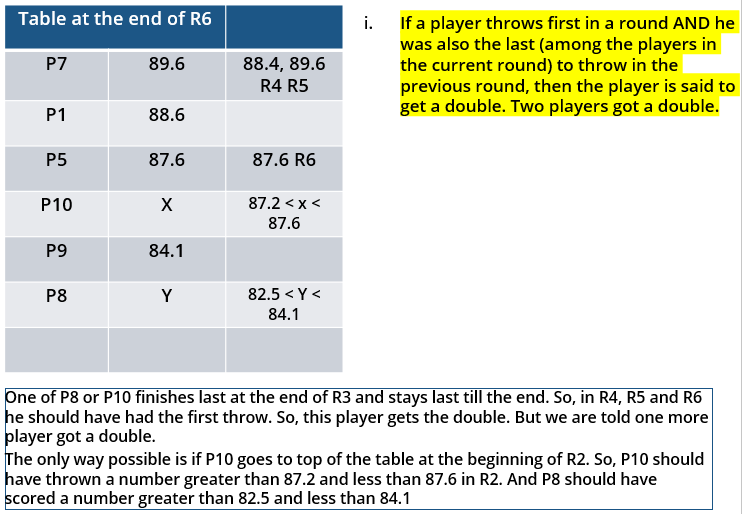
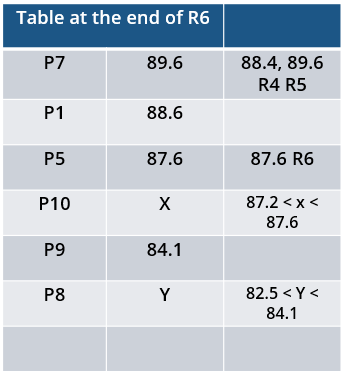
Which of the following can be the final score (in m) of P8?
Video Explanation
Explanatory Answer
By how much did the gold medalist improve his score (in m) in the second phase?
Video Explanation
Explanatory Answer
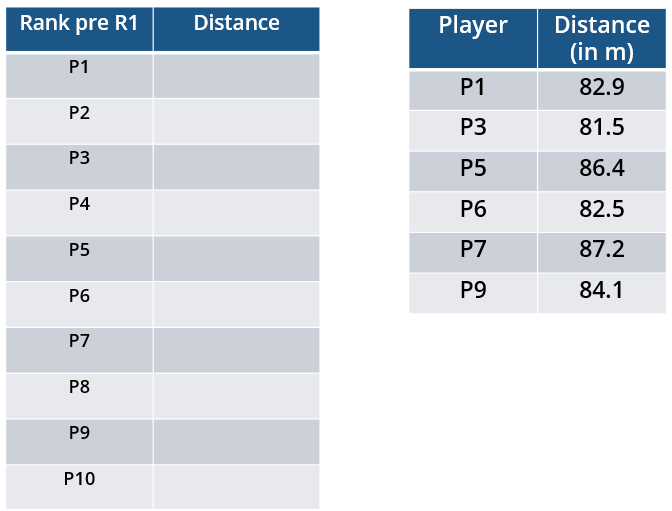
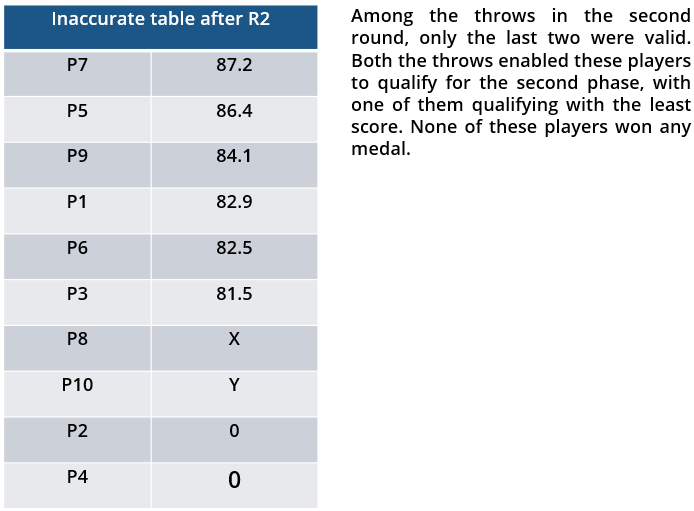
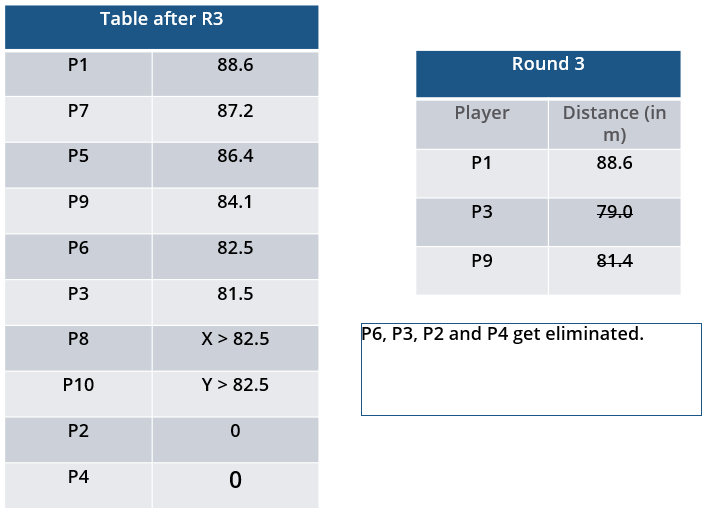
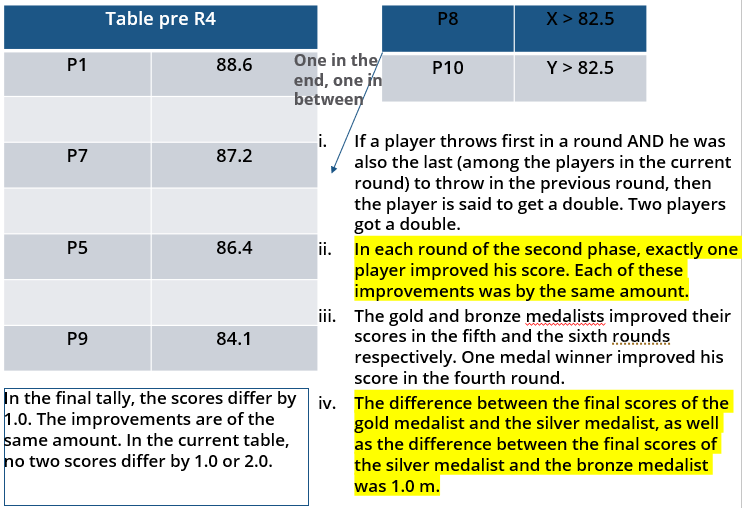
10 players – P1, P2, … , P10 - competed in an international javelin throw event. The number (after P) of a player reflects his rank at the beginning of the event, with rank 1 going to the topmost player. There were two phases in the event with the first phase consisting of rounds 1, 2, and 3, and the second phase consisting of rounds 4, 5, and 6. A throw is measured in terms of the distance it covers (in meters, up to one decimal point accuracy), only if the throw is a 'valid' one. For an invalid throw, the distance is taken as zero. A player's score at the end of a round is the maximum distance of all his throws up to that round. Players are re-ranked after every round based on their current scores. In case of a tie in scores, the player with a prevailing higher rank retains the higher rank. This ranking determines the order in which the players go for their throws in the next round.
In each of the rounds in the first phase, the players throw in increasing order of their latest rank, i.e. the player ranked 1 at that point throws first, followed by the player ranked 2 at that point and so on. The top six players at the end of the first phase qualify for the second phase. In each of the rounds in the second phase, the players throw in decreasing order of their latest rank i.e. the player ranked 6 at that point throws first, followed by the player ranked 5 at that point and so on. The players ranked 1, 2, and 3 at the end of the sixth round receive gold, silver, and bronze medals respectively.
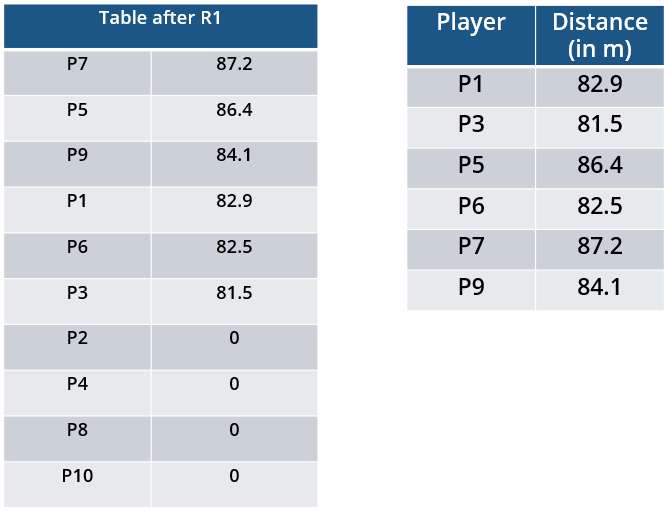
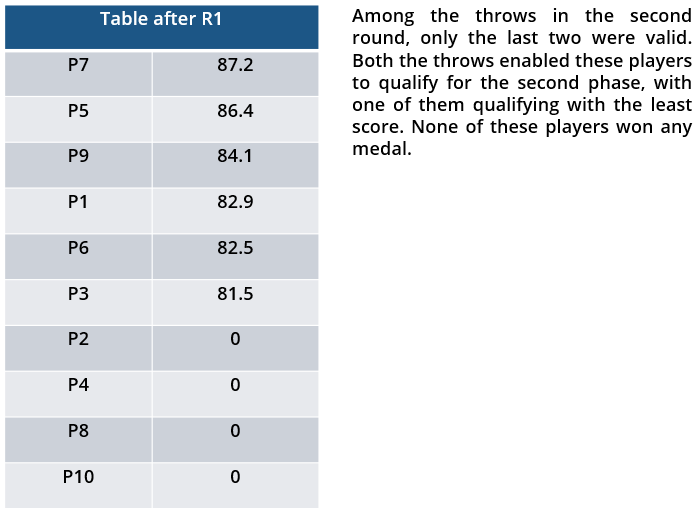
All the valid throws of the event were of distinct distances (as per stated measurement accuracy). The tables below show distances (in meters) covered by all valid throws in the first and the third round in the event.
Distances covered by all the valid throws in the first round
| Player | Distance (in m) |
| P1 | 82.9 |
| P3 | 81.5 |
| P5 | 86.4 |
| P6 | 82.5 |
| P7 | 87.2 |
| P9 | 84.1 |
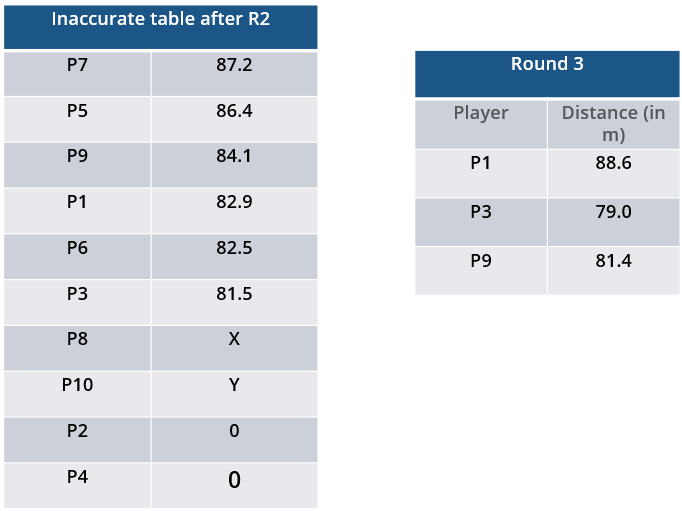
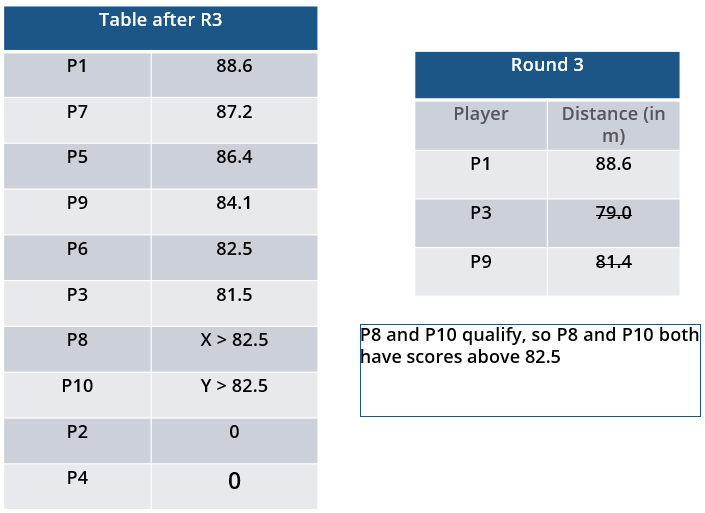
Distances covered by all the valid throws in the third round
| Player | Distance (in m) |
| P1 | 88.6 |
| P3 | 79.0 |
| P9 | 81.4 |
The following facts are also known.
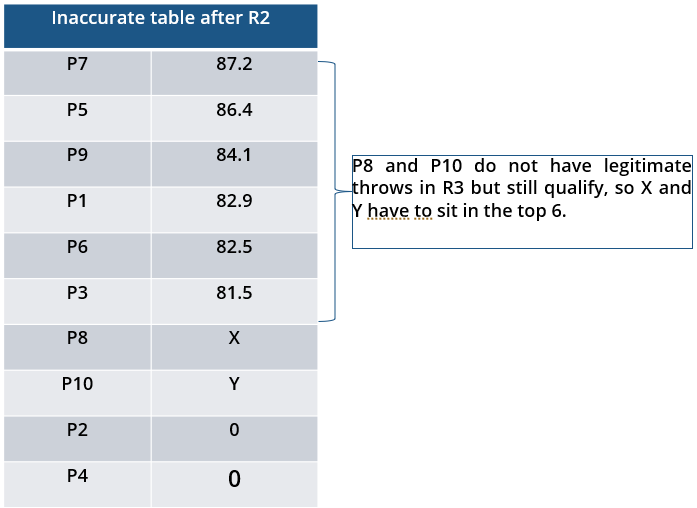
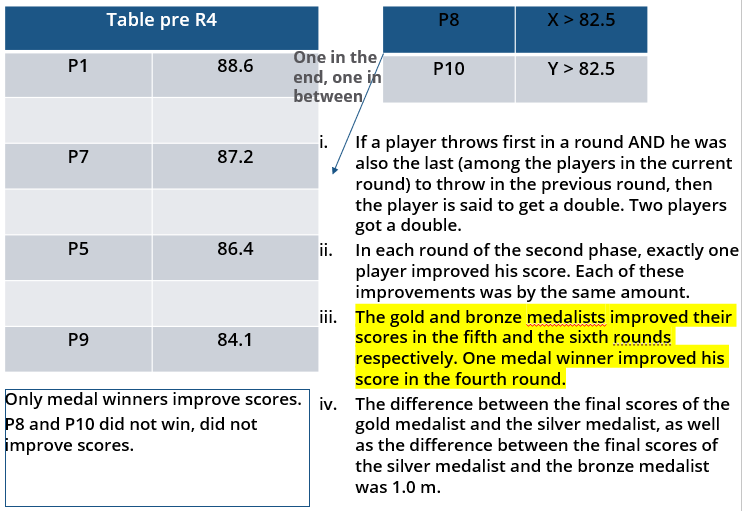
i. Among the throws in the second round, only the last two were valid. Both the throws enabled these players to qualify for the second phase, with one of them qualifying with the least score. None of these players won any medal.
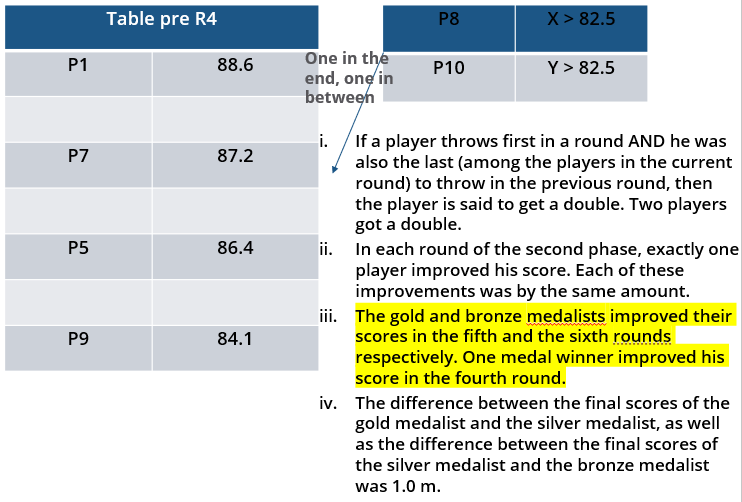
ii. If a player throws first in a round AND he was also the last (among the players in the current round) to throw in the previous round, then the player is said to get a double. Two players got a double.
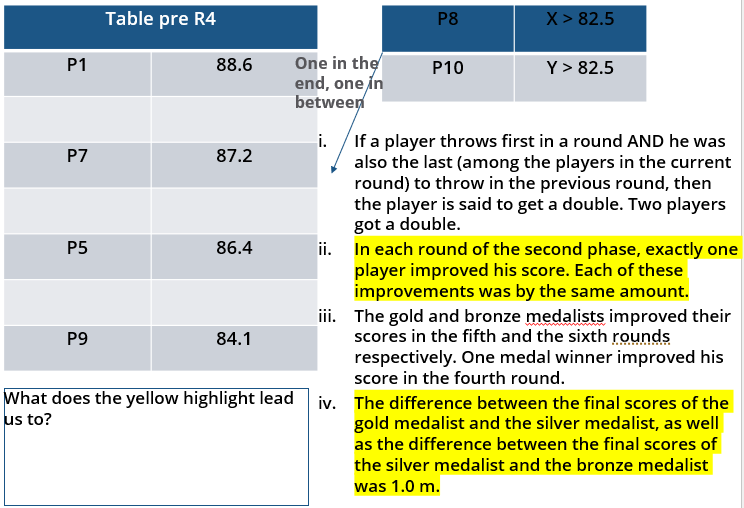
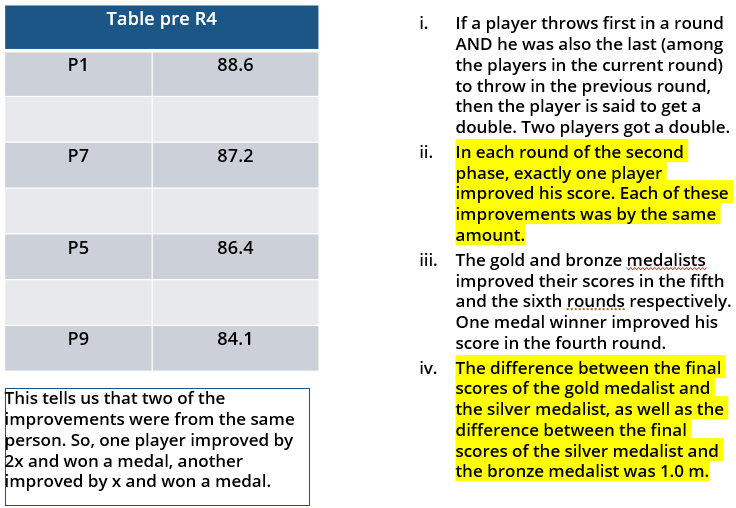
iii. In each round of the second phase, exactly one player improved his score. Each of these improvements was by the same amount.
iv. The gold and bronze medalists improved their scores in the fifth and the sixth rounds respectively. One medal winner improved his score in the fourth round.
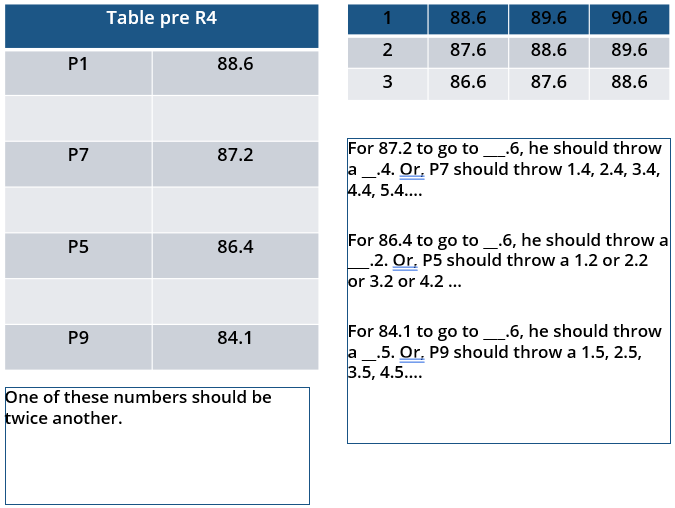
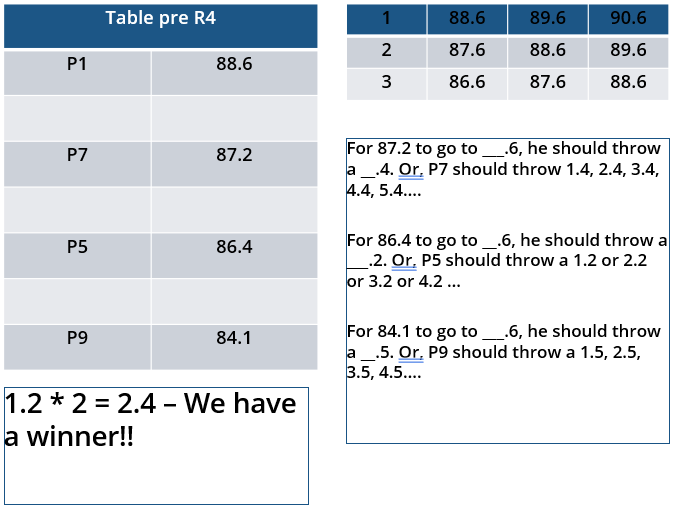
v. The difference between the final scores of the gold medalist and the silver medalist, as well as the difference between the final scores of the silver medalist and the bronze medalist was 1.0 m.
Which two players got the double?
Video Explanation
Explanatory Answer
Who threw the last javelin in the event?
Video Explanation
Explanatory Answer
What was the final score (in m) of the silver-medalist?
Video Explanation
Explanatory Answer
Which of the following can be the final score (in m) of P8?
Video Explanation
Explanatory Answer
By how much did the gold medalist improve his score (in m) in the second phase?
Video Explanation
Explanatory Answer
Which two players got the double?
Video Explanation
Explanatory Answer
Who threw the last javelin in the event?
Video Explanation
Explanatory Answer
The approval ratio of a reviewer is the ratio of the number of questions (s)he approved to the number of questions (s)he reviewed. Which option best describes Amal's approval ratio?
Video Explanation
Explanatory Answer
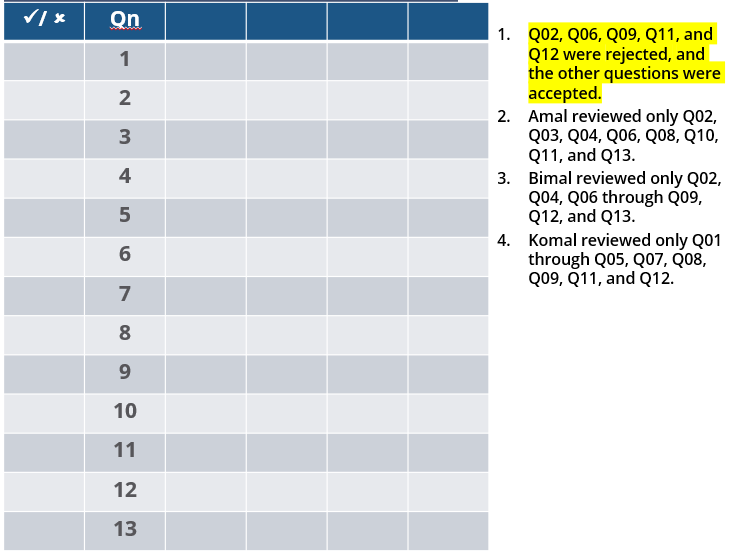
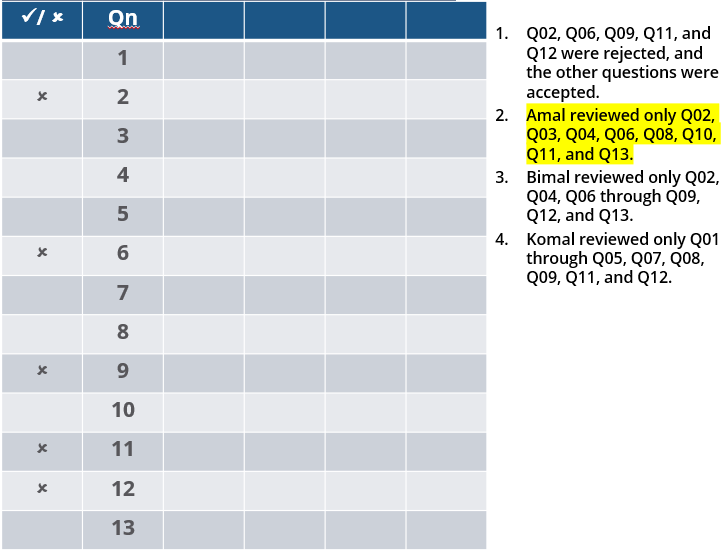
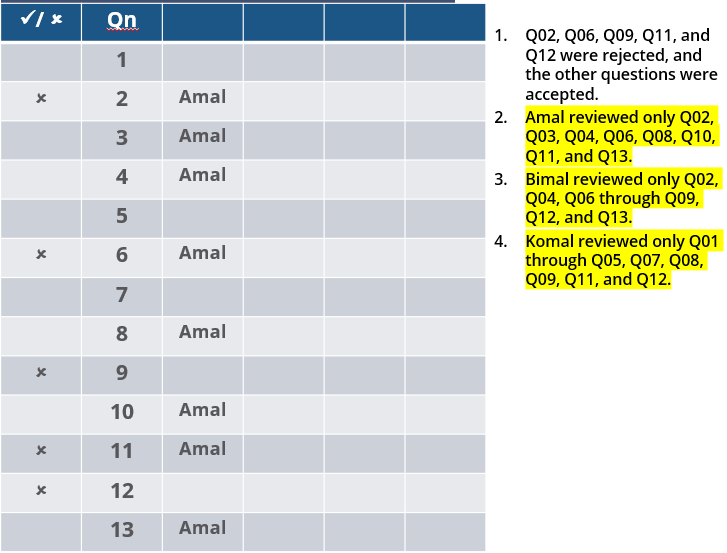
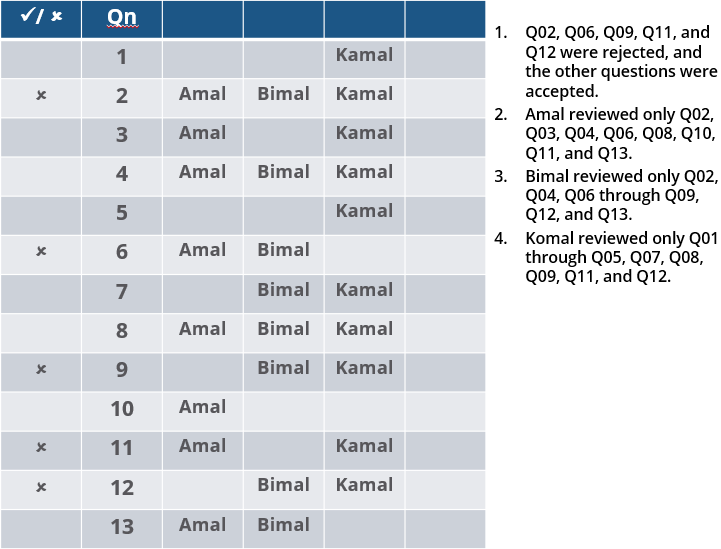
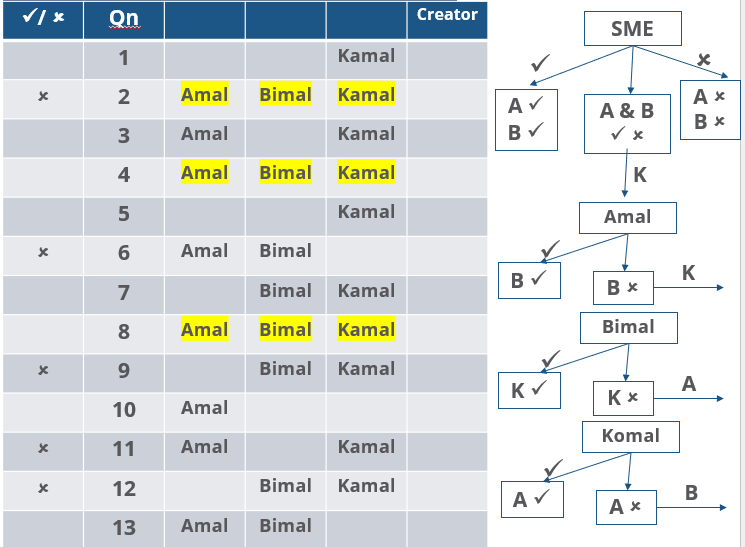
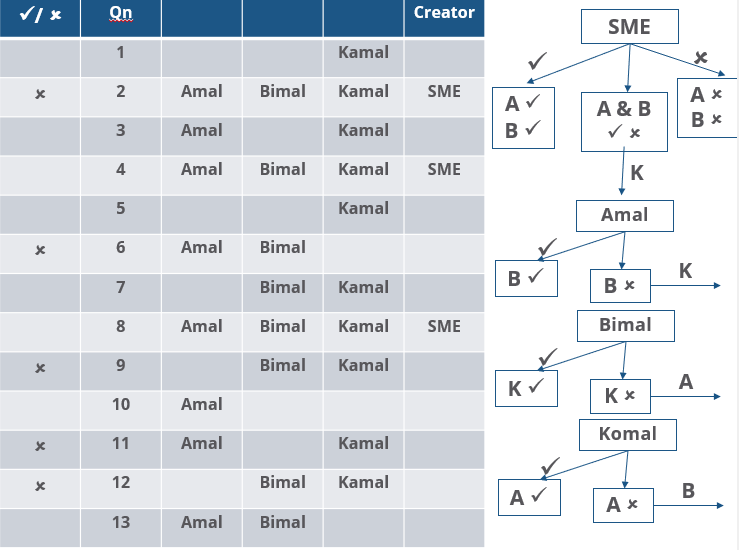
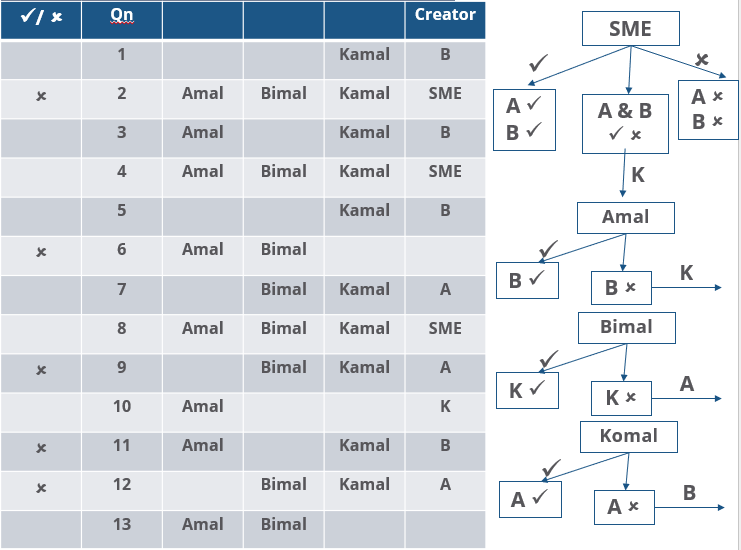
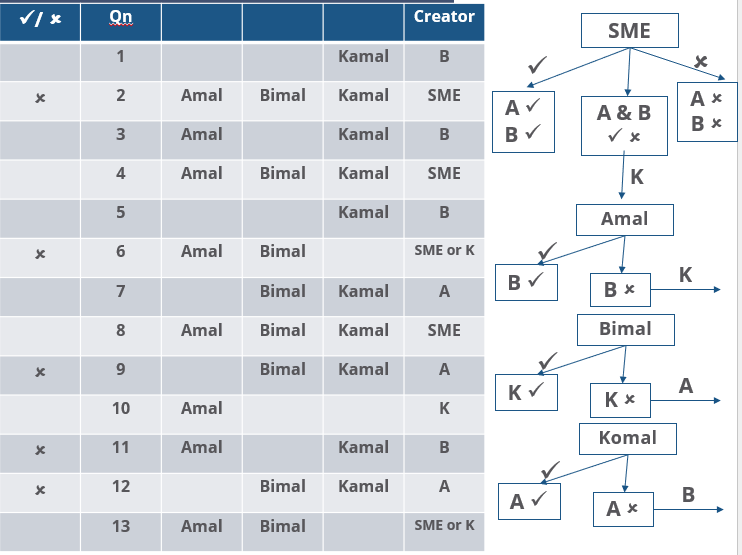
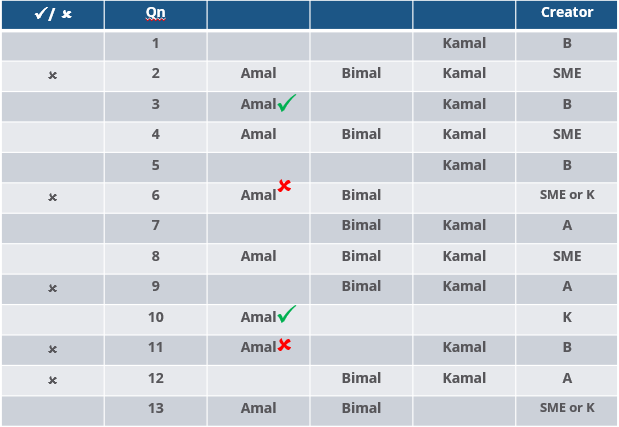
How many questions created by Amal or Bimal were disapproved by at least one of the other reviewers?
Video Explanation
Explanatory Answer
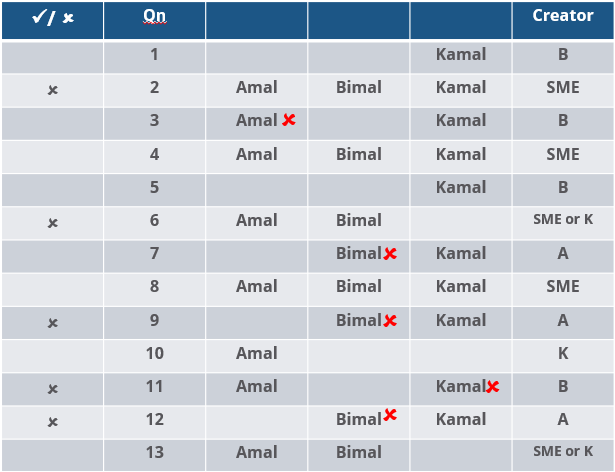
How many questions were DEFINITELY created by the SMEs?
Video Explanation
Explanatory Answer
How many questions were DEFINITELY disapproved by Bimal?
Video Explanation
Explanatory Answer
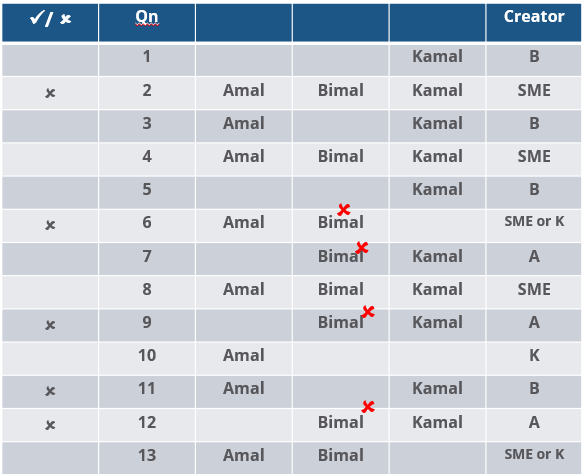
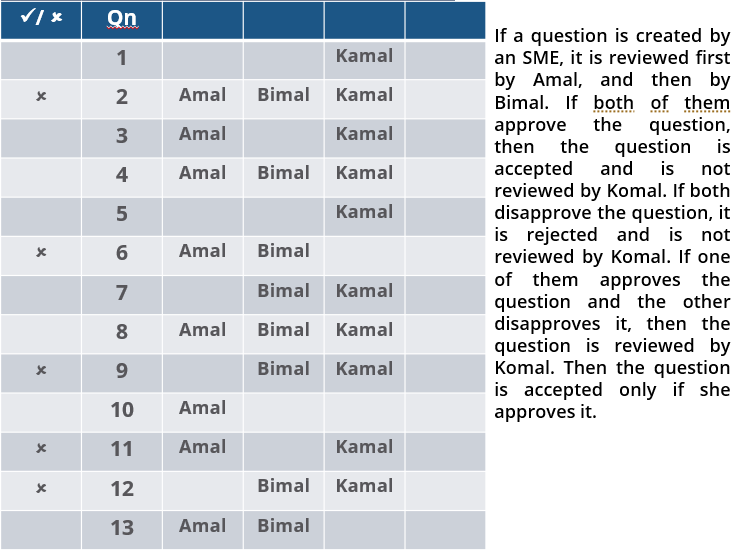
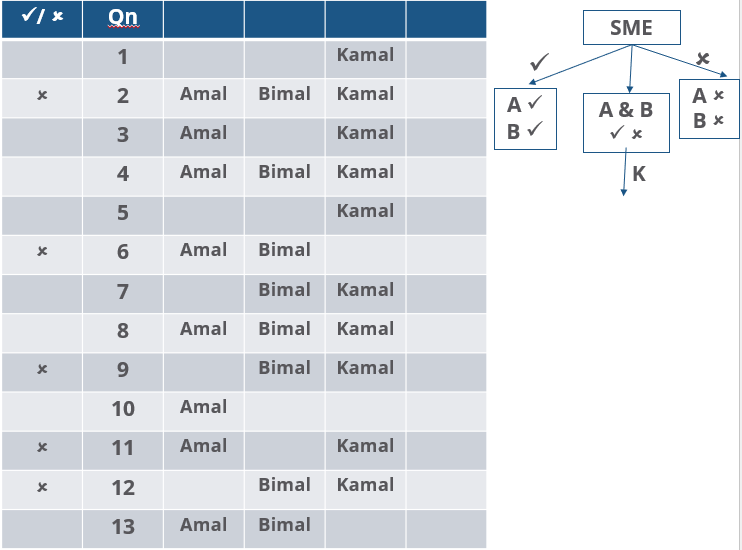
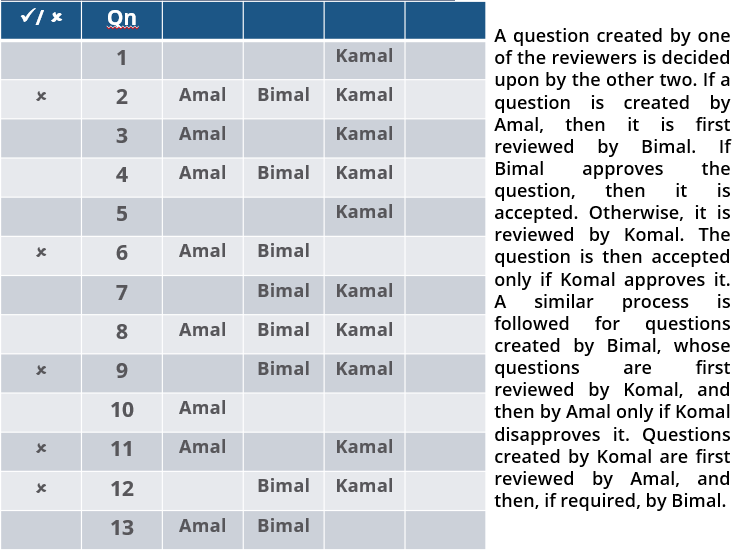
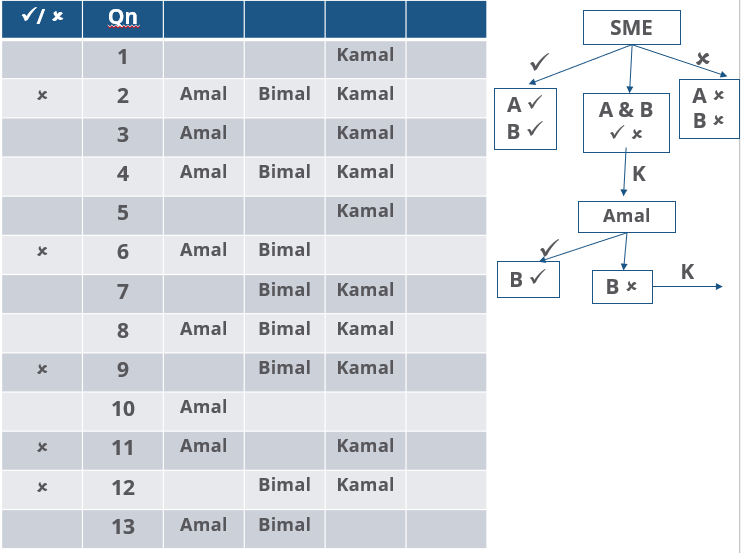
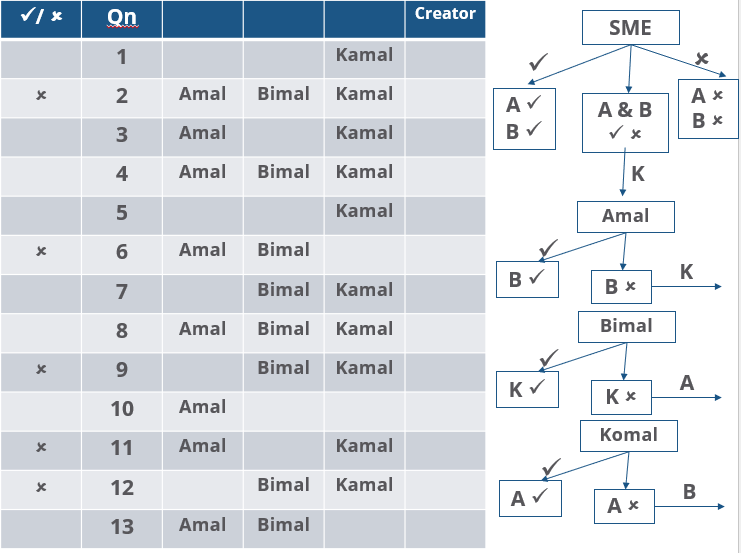
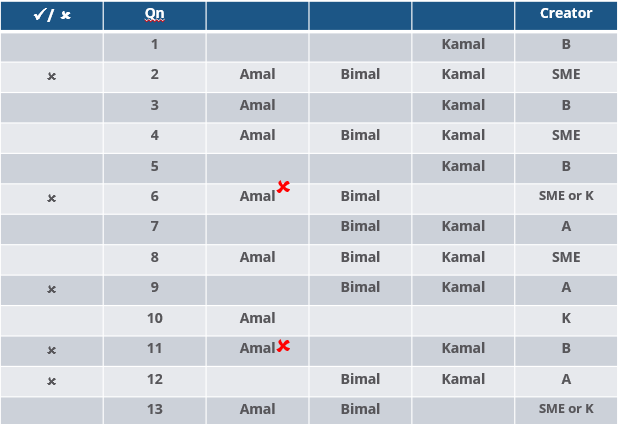
Three reviewers Amal, Bimal, and Komal are tasked with selecting questions from a pool of 13 questions (Q01 to Q13). Questions can be created by external "subject matter experts" (SMEs) or by one of the three reviewers. Each of the reviewers either approves or disapproves a question that is shown to them. Their decisions lead to eventual acceptance or rejection of the question in the manner described below.
If a question is created by an SME, it is reviewed first by Amal, and then by Bimal. If both of them approve the question, then the question is accepted and is not reviewed by Komal. If both disapprove the question, it is rejected and is not reviewed by Komal. If one of them approves the question and the other disapproves it, then the question is reviewed by Komal. Then the question is accepted only if she approves it.
A question created by one of the reviewers is decided upon by the other two. If a question is created by Amal, then it is first reviewed by Bimal. If Bimal approves the question, then it is accepted. Otherwise, it is reviewed by Komal. The question is then accepted only if Komal approves it. A similar process is followed for questions created by Bimal, whose questions are first reviewed by Komal, and then by Amal only if Komal disapproves it. Questions created by Komal are first reviewed by Amal, and then, if required, by Bimal.
The following facts are known about the review process after its completion.
1. Q02, Q06, Q09, Q11, and Q12 were rejected and the other questions were accepted.
2. Amal reviewed only Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
3. Bimal reviewed only Q02, Q04, Q06 through Q09, Q12, and Q13.
4. Komal reviewed only Q01 through Q05, Q07, Q08, Q09, Q11, and Q12.
How many questions were DEFINITELY created by Komal?
Video Explanation
Explanatory Answer
How many questions were DEFINITELY created by the SMEs?
Video Explanation
Explanatory Answer
How many questions were DEFINITELY disapproved by Bimal?
Video Explanation
Explanatory Answer
The approval ratio of a reviewer is the ratio of the number of questions (s)he approved to the number of questions (s)he reviewed. Which option best describes Amal's approval ratio?
Video Explanation
Explanatory Answer
How many questions created by Amal or Bimal were disapproved by at least one of the other reviewers?
Video Explanation
Explanatory Answer
How many questions were DEFINITELY created by Komal?
Video Explanation
Explanatory Answer
What BEST can be said about the distribution of object o1?
Video Explanation
Ten objects o1, o2, …, o10 were distributed among Amar, Barat, Charles, Disha, and Elise. Each item went to exactly one person. Each person got exactly two of the items, and this pair of objects is called her/his bundle.
The following table shows how each person values each object.
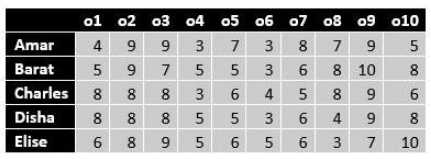
The value of any bundle by a person is the sum of that person's values of the objects in that bundle. A person X envies another person Y if X values Y's bundle more than X's own bundle.
For example, hypothetically suppose Amar's bundle consists of o1 and o2, and Barat's bundle consists of o3 and o4. Then Amar values his own bundle at 4 + 9 = 13 and Barat's bundle at 9 + 3 = 12. Hence Amar does not envy Barat. On the other hand, Barat values his own bundle at 7 + 5 = 12 and Amar's bundle at 5 + 9 = 14. Hence Barat envies Amar.
The following facts are known about the actual distribution of the objects among the five people.
1. If someone's value for an object is 10, then she/he received that object.
2. Objects o1, o2, and o3 were given to three different people.
3. Objects o1 and o8 were given to different people.
4. Three people value their own bundles at 16. No one values her/his own bundle at a number higher than 16.
5. Disha values her own bundle at an odd number. All others value their own bundles at an even number.
6. Some people who value their own bundles less than 16 envy some other people who value their own bundle at 16. No one else envies others.
What is Amar's value for his own bundle?
Video Explanation
What BEST can be said about the distribution of object o1?
Video Explanation
What is Amar's value for his own bundle?
Video Explanation
The natural numbers are divided into groups as (1), (2, 3, 4), (5, 6, 7, 8, 9), … and so on. Then, the sum of the numbers in the 15th group is equal to
Video Explanation
Explanatory Answer
The natural numbers are divided into groups as (1), (2, 3, 4), (5, 6, 7, 8, 9), ….. and so on.
If you observe that the first group ends with 12, the second group ends with 22and the third group ends with 32
Hence, the 15th group ends with 152 = 225.
The 14th group ends with 142 = 196.
Therefore, the 15th group contains (197, 198, . . . . . . . . . . ,225)
Amar, Akbar and Anthony are working on a project. Working together Amar and Akbar can complete the project in 1 year, Akbar and Anthony can complete in 16 months, Anthony and Amar can complete in 2 years. If the person who is neither the fastest nor the slowest works alone, the time in months he will take to complete the project is
Video Explanation
Explanatory Answer
Video Explanation
Explanatory Answer
How many three-digit numbers are greater than 100 and increase by 198 when the three digits are arranged in the reverse order?
Video Explanation
A circle of diameter 8 inches is inscribed in a triangle ABC where ∠ ABC= 90 °. If BC = 10 inches then the area of the triangle in square inches is
Video Explanation
Explanatory Answer
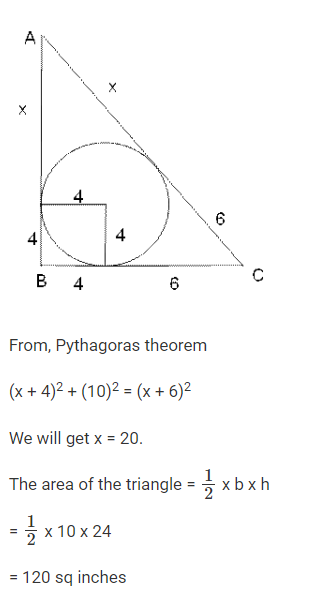
Onion is sold for 5 consecutive months at the rate of Rs 10, 20, 25, 25, and 50 per kg, respectively. A family spends a fixed amount of money on onion for each of the first three months, and then spends half that amount on onion for each of the next two months. The average expense for onion, in rupees per kg, for the family over these 5 months is closest to
Video Explanation
Explanatory Answer
Given that onion is sold for 5 consecutive months at the rate of Rs 10, 20, 25, 25, and 50 per kg respectively.
Let’s consider the amount spend on onions in these five months to be 100, 100, 100, 50, 50.
Hence, the number of kgs in these five months should be 10, 5, 4, 2, 1 respectively.
The average expense on onions per kg over these five months is given by
Therefore, the closest average would be 18.
Two trains cross each other in 14 seconds when running in opposite directions along parallel tracks. The faster train is 160 m long and crosses a lamp post in 12 seconds. If the speed of the other train is 6 km/hr less than the faster one, its length, in m, is
Video Explanation
Video Explanation
Amal purchases some pens at ₹ 8 each. To sell these, he hires an employee at a fixed wage. He sells 100 of these pens at ₹ 12 each. If the remaining pens are sold at ₹ 11 each, then he makes a net profit of ₹ 300, while he makes a net loss of ₹ 300 if the remaining pens are sold at ₹ 9 each. The wage of the employee, in INR, is
Video Explanation
Suppose the length of each side of a regular hexagon ABCDEF is 2 cm. If T is the midpoint of CD, then the length of AT, in cm, is
Video Explanation
Explanatory Answer
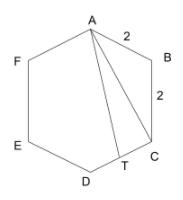
In a regular hexagon, each internal angle is equal to 120°.
From isosceles triangle ABC, we know the length of two sides and including angle.
We will be able to find the third side (AC) using the Pythagoras theorem or the sine rule.
Hence, AC = 2√3cm
Given that, T is the midpoint.
So, CT = 1cm.
From the right-angled △ ACT,
AC2 + CT2 = AT2
AT2 = (2 √3)2 + (1)2 = 13
AT = √(13)
Video Explanation
Explanatory Answer
Suppose hospital A admitted 21 less Covid infected patients than hospital B, and all eventually recovered. The sum of recovery days for patients in hospitals A and B were 200 and 152, respectively. If the average recovery days for patients admitted in hospital A was 3 more than the average in hospital B then the number admitted in hospital A was
Video Explanation
Explanatory Answer
Let's consider the number of patients admitted in hospital A and hospital B to be 'x' and ‘x + 21'
Given that, the sum of recovery days for patients in hospitals A and B were 200 and 152, respectively.
The average recovery days for patients admitted in hospital A was 3 more than the average in-hospital B.
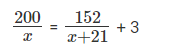
By solving the above equation we get x = 35.
Hence, the number of patients admitted to hospital A is 35.
Anu, Vinu and Manu can complete a work alone in 15 days, 12 days and 20 days, respectively. Vinu works everyday. Anu works only on alternate days starting from the first day while Manu works only on alternate days starting from the second day. Then, the number of days needed to complete the work is
Video Explanation
Explanatory Answer
The amount Neeta and Geeta together earn in a day equals what Sita alone earns in 6 days. The amount Sita and Neeta together earn in a day equals what Geeta alone earns in 2 days. The ratio of the daily earnings of the one who earns the most to that of the one who earns the least is
Video Explanation
Identical chocolate pieces are sold in boxes of two sizes, small and large. The large box is sold for twice the price of the small box. If the selling price per gram of chocolate in the large box is 12% less than that in the small box, then the percentage by which the weight of chocolate in the large box exceeds that in the small box is nearest to
Video Explanation
Explanatory Answer
Let's consider the selling prices of small and large chocolate boxes be ‘x’ and ‘2x’ respectively.
Let's also consider the weights of the small and large chocolate boxes to be 100(to make it easy) and y respectively.
Given that, the selling price per gram of chocolate in the large box is 12% less than that in the small box.
Therefore,
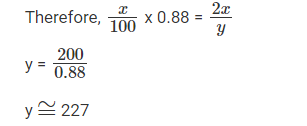
Hence, the weight of chocolate in a large box exceeds 127% of that of a small box.
Hence the answer is 127.
f(x) = \({x^{2}+2x-15 \over {x^{2}-7x-18}}\) is negative if and only if
Video Explanation
Explanatory Answer
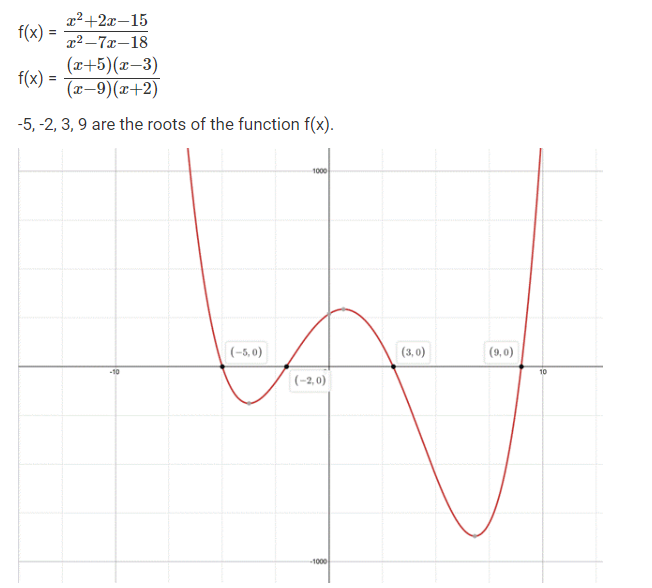
Keeping these roots on the number line and checking for the range where f(x) becomes negative.
For the numbers below -5, f(x) is positive.
For the numbers between -5 and -2, the value f(x) is negative.
For the numbers between -2 and 3, the value of f(x) is positive.
For the numbers between 3 and 9, the value of f(x) is negative.
For the numbers above 9, the value of f(x) is positive.
Hence the range should be -5 < x < -2 and 3 < x < 9.
A basket of 2 apples, 4 oranges and 6 mangoes costs the same as a basket of 1 apple, 4 oranges and 8 mangoes, or a basket of 8 oranges and 7 mangoes. Then the number of mangoes in a basket of mangoes that has the same cost as the other baskets is23301
Video Explanation
Explanatory Answer
The number of integers n that satisfy the inequalities |n-60| < |n-100| < |n-20| is
Video Explanation
If the area of a regular hexagon is equal to the area of an equilateral triangle of side 12 cm, then the length, in cm, of each side of the hexagon is
Video Explanation
Explanatory Answer
The strength of an indigo solution in percentage is equal to the amount of indigo in grams per 100 cc of water. Two 800 cc bottles are filled with indigo solutions of strengths 33% and 17%, respectively. A part of the solution from the first bottle is thrown away and replaced by an equal volume of the solution from the second bottle. If the strength of the indigo solution in the first bottle has now changed to 21% then the volume, in cc, of the solution left in the second bottle is
Video Explanation
Explanatory Answer
Given that, there are two 800cc bottles of indigo solution with strengths of 33% and 17% respectively.
Some amount of the solution from bottle 1 is replaced by the same amount of solution from bottle 2.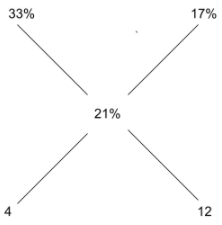
In 800cc of a new solution of strength 21% has two solutions in the ratio 1:3.
200cc of 33% solution and 600cc of 17% solution combined to give 21% solution of indigo
Hence, the remaining solution in the bottle 2 is 200cc.
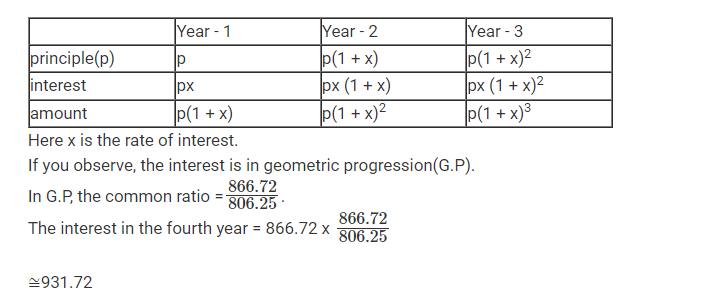
Anil invests some money at a fixed rate of interest, compounded annually. If the interests accrued during the second and third year are ₹ 806.25 and ₹ 866.72, respectively, the interest accrued, in INR, during the fourth year is nearest to
Video Explanation
Explanatory Answer
Anil can paint a house in 12 days while Barun can paint it in 16 days. Anil, Barun, and Chandu undertake to paint the house for ₹ 24000 and the three of them together complete the painting in 6 days. If Chandu is paid in proportion to the work done by him, then the amount in INR received by him is
Video Explanation
Explanatory Answer
