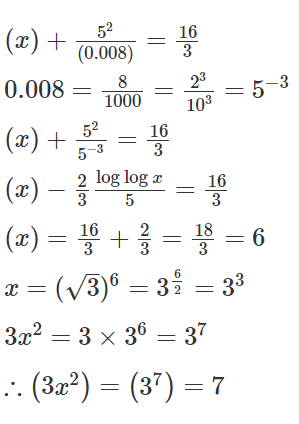Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
495
Learners
asked the doubt

Previous Year Questions
Five students, including Amit, appear for an examination in which possible marks are integers between 0 and 50, both inclusive. The average marks for all the students is 38 and exactly three students got more than 32. If no two students got the same marks and Amit got the least marks among the five students, then the difference between the highest and lowest possible marks of Amit is
Video Explanation

Explanatory Answer
The case where Amit gets the least amount of marks looks like…
The maximum mark that Amit can get is 31, He can get it if he can grab 20 marks from the people who score 48, 49 and 50.
In fact, it is possible for Amit to do that…
The difference between the highest and lowest marks if Amit = 31 - 11 = 20.
In an examination, there were 75 questions. 3 marks were awarded for each correct answer, 1 mark was deducted for each wrong answer and 1 mark was awarded for each unattempted question. Rayan scored a total of 97 marks in the examination. If the number of unattempted questions was higher than the number of attempted questions, then the maximum number of correct answers that Rayan could have given in the examination is
Video Explanation

Explanatory Answer
The rules of the examination are…
● A correct answer gets +3 marks.
● A wrong answer gets -1 mark.
● An unanswered question gets +1 mark.
So, the scenario is, every question is already awarded 1 mark before attempting, if the attempt is right you get +2 marks and if it is wrong you get -2 marks.
So after re-imagining the examination…
● Every Question is awarded + 1 before attempting itself.
(This means you enter the examination with 75 marks in your pocket)
● A right answer fetches +2 marks.
● A wrong answer fetches -2 marks.
Now it is up to the student to increase or decrease his total marks from 75.
If he answers more questions right than wrong he gets additional marks.
If he answers more questions wrong than right his marks decrease.
So, when Rayan scored a total of 97 marks in the examination, 75 were given to him on a platter. The remaining 22 is what he put effort to score.
This means the difference between the number of questions he got right and the number of questions he got wrong is 11.
In the most extreme case, he might have got 11 questions right and did not attempt the remaining.
| Right | Wrong | Unattempted |
| 11 | 0 | 64 |
He might have got a few questions wrong, but the number of right questions should always be more than the number of wrong questions by 11.
The case where the number of wrong questions is ‘x’ looks like…
| Right | Wrong | Unattempted |
| 11 + x | x | 64 - 2x |
The number of unattempted questions was higher than the number of attempted questions…
This means,
64 - 2x > 11 + x + x
53 > 4x
x≤13x≤13.
The maximum value of x is 13.
The maximum number of the right answers = 11 + 13 = 24
The number of integers greater than 2000 that can be formed with the digits 0, 1, 2, 3, 4, 5, using each digit at most once, is
Video Explanation

Explanatory Answer
The number of 6-digit integers that can be formed is 600.
The number of 5-digit integers that can be formed is 600.
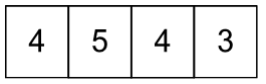
The number of 4-digit integers that can be formed is 240.
The total number of integers greater than 2000 that can be formed with the digits 0, 1, 2, 3, 4, 5,
using each digit at most once, is 600 + 600 + 240 = 1440
In an election, there were four candidates and 80% of the registered voters casted their votes. One of the candidates received 30% of the casted votes while the other three candidates received the remaining casted votes in the proportion 1 : 2 : 3. If the winner of the election received 2512 votes more than the candidate with the second highest votes, then the number of registered voters was
Video Explanation

Explanatory Answer
One candidate got 30% of the polled votes, the remaining three got in the ratio of 1 : 2 : 3
The polled votes were split in 3 : 7 ratio.
The 70% of them were again split in the ratio 1 : 2 : 3
The votes were polled in the ratio of 6(3) : 7(1 : 2 : 3)
18 : 7 : 14 : 21
Let’s assume that the actual polled votes are 18x, 7x, 14x, 21x
The winner of the election received 2512 votes more than the candidate with the second highest votes.
21x - 18x = 2512
3x = 2512
Total polled votes = 18x + 7x + 14x + 21x = 60x = 20(3x) = 20(2512) = 50,240
The polled votes represent 80% of the total registered votes.
Total registered votes = 50,240 + 12,560 = 62,800.
The average of a non-decreasing sequence of N numbers a1,a2,…,aN is 300 . If a1 is replaced by 6a1, the new average becomes 400. Then, the number of possible values of a1 is
Video Explanation

Explanatory Answer
a1 + a2 + a3 + … + an = 300(n)
6a1 + a2 + a3 + … + an = 400(n)
5a1 = 100(n)
a1 = 20(n)
The constraints of the problem are:
● Sum of n terms = 300(n)
● The first term is 20(n)
● All other terms (terms other than the first term) should be greater than or equal to the first term. (Because the sequence is a non-decreasing sequence.)
Image a scenario where all the other terms are equal to the first term. That is a case where all the terms are equal. Since the average is 300. All of them should be 300. The first term is 300.
20(n) = 300
n = 15
Now imagine that the sequence has 16 terms the first term will be 320, and all the other terms will be greater than or equal to 320. So the average can’t be 300.
Or basically, the maximum number of terms in the sequence is 15.
What is the minimum number of terms in the sequence?
Can the sequence have one term?
n = 1
a1 = 20
But the sum of terms is not 300.
The sequence should have more than one term.
n = 2
a1 = 2(20) = 40
The sum of terms can be 300(2). This happens by having the second term as 560.
The minimum number of terms in the sequence is 2.
The maximum number of terms in the sequence is 15.
The number of terms in the sequence can have 14 different values.
And in each case the value of a1 is distinct.
Hence, a1 can have 14 different values.
On day one, there are 100 particles in a laboratory experiment. On day n, where n≥2, one out of every n particles produces another particle. If the total number of particles in the laboratory experiment increases to 1000 on day m, then m equals
Video Explanation

Explanatory Answer

There are two containers of the same volume, first container half-filled with sugar syrup and the second container half-filled with milk. Half the content of the first container is transferred to the second container, and then the half of this mixture is transferred back to the first container. Next, half the content of the first container is transferred back to the second container. Then the ratio of sugar syrup and milk in the second container is
Video Explanation

Explanatory Answer
Let the half volume of each container be 80 cc.
Why 80cc though? Why not some other value?
We know that the process of shifting half volumes is happening three times overall.
(12)3=18(12)3=18.
So it would be wise to assume the initial volume to be some multiple of 8 so that we don’t have to deal with fractions later on.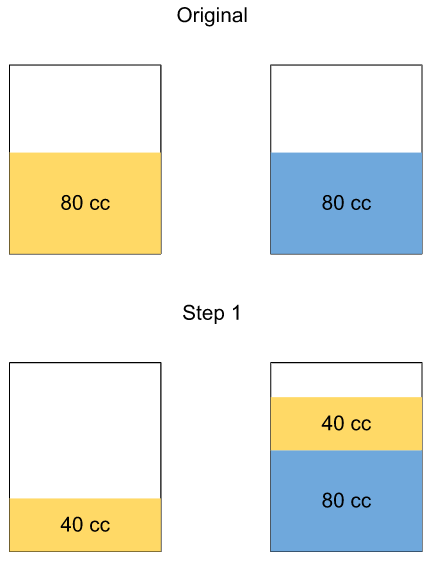
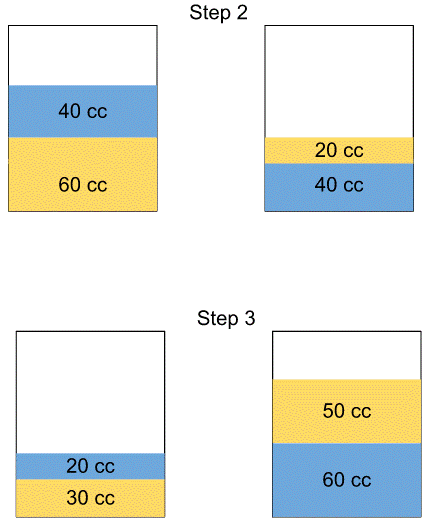
The ratio of Sugar Syrup to Water in the second container is 5 : 6.
Manu earns ₹4000 per month and wants to save an average of ₹550 per month in a year. In the first nine months, his monthly expense was ₹3500, and he foresees that, tenth month onward, his monthly expense will increase to ₹3700. In order to meet his yearly savings target, his monthly earnings, in rupees, from the tenth month onward should be
Video Explanation

Explanatory Answer
On average, Manu targets saving ₹550 per month.
In the first 9 months, Manu earns ₹4000 per month and spends ₹3500.
So, he ends up saving only ₹450 per month. In other words, he misses his target by ₹50 per month.
So he saves ₹50 ×× 9 = ₹450 less than his target.
In the next 3 months of the year, his expenses are ₹3700 per month. To save ₹550 per month in these three months, his income should be ₹3700 + ₹550 = ₹4250 per month.
But also, he should earn some more to compensate for the ₹450 he was short of in the first 9 months. This ₹450 is earned over a span of 3 months. Or he should earn ₹150 extra each month.
So Manu’s income in the last 3 months = ₹4250 + ₹150 = ₹4400
If a and b are non-negative real numbers such that a+2b=6, then the average of the maximum and minimum possible values of (a+b) is
Video Explanation

Explanatory Answer
a + 2b = 6
a + b = 6 - b
Clearly, the maximum/minimum value of (a + b) depends on the value of b.
Since a and b are positive real numbers,
The minimum value that b can take is 0.
The maximum value that b can take is when a is 0.
0 + 2b = 6
b = 3.
When b = 0; a + b = 6 - b = 6
When b = 3; a + b = 6 - 3 = 3
Therefore, the minimum and maximum values of (a + b) are 3 and 6 respectively.
The average of these extreme values is ( 3 + 6)/2
Regular polygons A and B have number of sides in the ratio 1 : 2 and interior angles in the ratio 3 : 4. Then the number of sides of B equals
Video Explanation

Explanatory Answer

Working alone, the times taken by Anu, Tanu and Manu to complete any job are in the ratio 5 : 8 : 10. They accept a job which they can finish in 4 days if they all work together for 8 hours per day. However, Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day. Then, the number of hours that Manu will take to complete the remaining job working alone is
Video Explanation

Explanatory Answer
Time taken by Anu, Tanu and Manu to complete a job is in the ratio 5 : 8 : 10
This means that their efficiencies are in the ratio 15 : 18 : 110
Or, their efficiencies are in the ratios 8 : 5 : 4
This means, for instance, if Anu can wash 8 plates in an hour, Tanu and Manu can wash 5 & 4
plates respectively in one hour.
So, let us remodel the entire question over this imaginary scenario of washing plates…
All three of them finish the job in 4 days working 8 hours per day.
Anu, Tanu and Manu can wash 8, 5 and 4 plates respectively in an hour.
So the total number of plates = (8+5+4)×4×8=17×4×8
Anu and Tanu work together for 6 days, working 6 hours 40 minutes per day.
The total number of plates washed by them = (8+5)×6×623=13×40
So the remaining plates to be washed =17×4×8−13×40
=4(17×8−130)
=4(80+56−130)
=4×6
So, the question is, in how many hours can Manu wash 4×6 plates?
We know that Manu can wash 4 plates in one hour.
Therefore, he requires 6 hours to wash 4×6 plates.
Profit per employee is the ratio of a company's profit to its employee strength. For this purpose, the employee strength in a year is the average of the employee strength at the beginning of that year and the beginning of the next year. In 2020, which of the four companies had the highest profit per employee?
Video Explanation

Explanatory Answer
The answer is 'Company B'
Choice A is the correct answer.
The two plots below show data for four companies code-named A, B, C, and D over three years - 2019, 2020, and 2021.
The first plot shows the revenues and costs incurred by the companies during these years. For example, in 2021, company C earned Rs.100 crores in revenue and spent Rs.30 crores. The profit of a company is defined as its revenue minus its costs.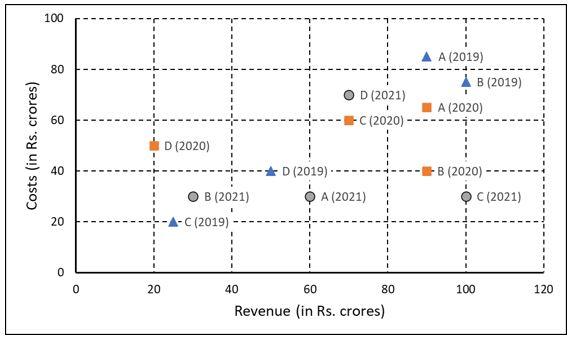
The second plot shows the number of employees employed by the company (employee strength) at the start of each of these three years, as well as the number of new employees hired each year (new hires). For example, Company B had 250 employees at the start of 2021, and 30 new employees joined the company during the year.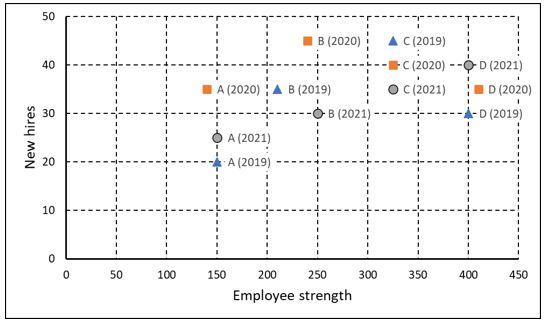
Considering all three years, which company had the highest annual profit?
Video Explanation

Explanatory Answer
It is given,
Company A:
Revenue = 240 and cost incurred = 180
Profit = 240 - 180 = 60
Company B:
Revenue = 220 and cost incurred = 145
Profit = 220 - 145 = 75
Company C:
Revenue = 195 and cost incurred = 110
Profit = 195 - 110 = 85
Company D: Revenue = 140 and cost incurred = 160
No profit.
Company C had the highest annual profit.
The question is " Considering all three years, which company had the highest annual profit? "
Hence, the answer is 'Company C'
Choice A is the correct answer.
Which of the four companies experienced the highest annual loss in any of the years?
Video Explanation

Explanatory Answer
For all the companies in all three years, cost incurred is less than Revenue except for D in 2020.
Revenue is 20 and cost incurred is 50
Company D experienced the highest annual loss in 2020
The question is " Which of the four companies experienced the highest annual loss in any of the years? "
Hence, the answer is 'Company D'
Choice A is the correct answer.
The ratio of a company's annual profit to its annual costs is a measure of its performance. Which of the four companies had the lowest value of this ratio in 2019?
Video Explanation

Explanatory Answer
The question is " The ratio of a company's annual profit to its annual costs is a measure of its performance. Which of the four companies had the lowest value of this ratio in 2019? "
Hence, the answer is 'Company A'
Choice A is the correct answer.
The total number of employees lost in 2019 and 2020 was the least for:
Video Explanation

Explanatory Answer
Company A:
The number of employees in the beginning of 2019 = 150
The number of employees hired in 2019 = 20
The number of employees should be at the beginning of 2020 is 150+20, i.e. 170 but there are 140 only. This
implies 30 left company A in 2019.
The number of employees in the beginning of 2020 = 140
The number of employees hired in 2020 = 35
The number of employees should be at the beginning of 2021 is 140+35, i.e. 175 but there are 150 only. This
implies 25 left company A in 2020.
The number of employees left company A in 2019 and 2020 = 30 + 25 = 55
Company B:
Similarly, the number of employees left company B in 2019 = 210 + 35 - 240 = 5
The number of employees left company B in 2020 = 240 + 45 - 250 = 35
The number of employees left company B in 2019 and 2020 = 5 + 35 = 40
Company C:
Similarly, the number of employees left company C in 2019 = 320 + 45 - 320 = 45
The number of employees left company C in 2020 = 320 + 40 - 320 = 40
The number of employees left company C in 2019 and 2020 = 45 + 40 = 85
Company D:
Similarly, the number of employees left company D in 2019 = 400 + 30 - 410 = 20
The number of employees left company D in 2020 = 410 + 35 - 400 = 45
The number of employees left company D in 2019 and 2020 = 20 + 45 = 65
The total number of employees lost in 2019 and 2020 is least for company B.
Profit per employee is the ratio of a company's profit to its employee strength. For this purpose, the employee strength in a year is the average of the employee strength at the beginning of that year and the beginning of the next year. In 2020, which of the four companies had the highest profit per employee?
Video Explanation

Explanatory Answer
The answer is 'Company B'
Choice A is the correct answer.
Considering all three years, which company had the highest annual profit?
Video Explanation

Explanatory Answer
It is given,
Company A:
Revenue = 240 and cost incurred = 180
Profit = 240 - 180 = 60
Company B:
Revenue = 220 and cost incurred = 145
Profit = 220 - 145 = 75
Company C:
Revenue = 195 and cost incurred = 110
Profit = 195 - 110 = 85
Company D: Revenue = 140 and cost incurred = 160
No profit.
Company C had the highest annual profit.
The question is " Considering all three years, which company had the highest annual profit? "
Hence, the answer is 'Company C'
Choice A is the correct answer.
Which of the four companies experienced the highest annual loss in any of the years?
Video Explanation

Explanatory Answer
For all the companies in all three years, cost incurred is less than Revenue except for D in 2020.
Revenue is 20 and cost incurred is 50
Company D experienced the highest annual loss in 2020
The question is " Which of the four companies experienced the highest annual loss in any of the years? "
Hence, the answer is 'Company D'
Choice A is the correct answer.
The ratio of a company's annual profit to its annual costs is a measure of its performance. Which of the four companies had the lowest value of this ratio in 2019?
Video Explanation

Explanatory Answer
The question is " The ratio of a company's annual profit to its annual costs is a measure of its performance. Which of the four companies had the lowest value of this ratio in 2019? "
Hence, the answer is 'Company A'
Choice A is the correct answer.
The total number of employees lost in 2019 and 2020 was the least for:
Video Explanation

Explanatory Answer
Company A:
The number of employees in the beginning of 2019 = 150
The number of employees hired in 2019 = 20
The number of employees should be at the beginning of 2020 is 150+20, i.e. 170 but there are 140 only. This
implies 30 left company A in 2019.
The number of employees in the beginning of 2020 = 140
The number of employees hired in 2020 = 35
The number of employees should be at the beginning of 2021 is 140+35, i.e. 175 but there are 150 only. This
implies 25 left company A in 2020.
The number of employees left company A in 2019 and 2020 = 30 + 25 = 55
Company B:
Similarly, the number of employees left company B in 2019 = 210 + 35 - 240 = 5
The number of employees left company B in 2020 = 240 + 45 - 250 = 35
The number of employees left company B in 2019 and 2020 = 5 + 35 = 40
Company C:
Similarly, the number of employees left company C in 2019 = 320 + 45 - 320 = 45
The number of employees left company C in 2020 = 320 + 40 - 320 = 40
The number of employees left company C in 2019 and 2020 = 45 + 40 = 85
Company D:
Similarly, the number of employees left company D in 2019 = 400 + 30 - 410 = 20
The number of employees left company D in 2020 = 410 + 35 - 400 = 45
The number of employees left company D in 2019 and 2020 = 20 + 45 = 65
The total number of employees lost in 2019 and 2020 is least for company B.
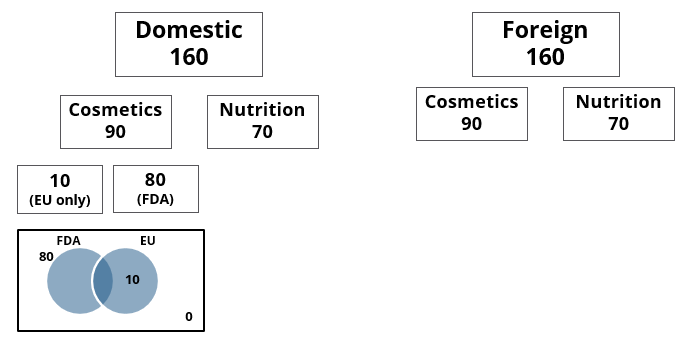
A speciality supermarket sells 320 products. Each of these products was either a cosmetic product or a nutrition product. Each of these products was also either a foreign product or a domestic product. Each of these products had at least one of the two approvals – FDA or EU.
The following facts are also known:
1. There were equal numbers of domestic and foreign products.
2. Half of the domestic products were FDA approved cosmetic products.
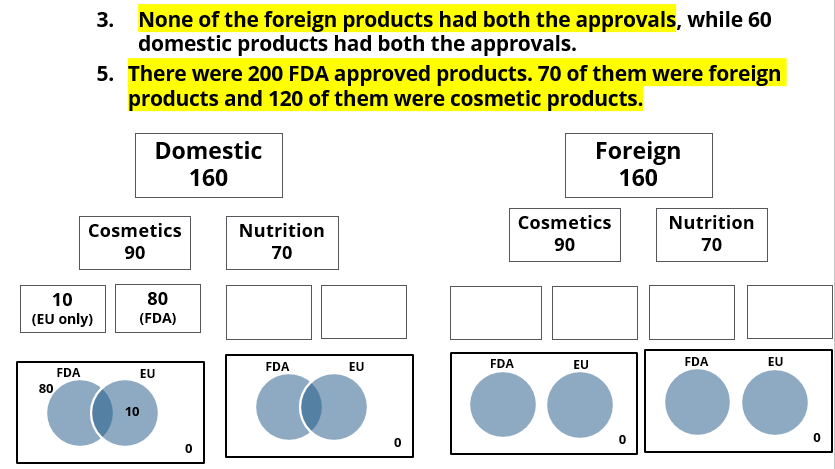
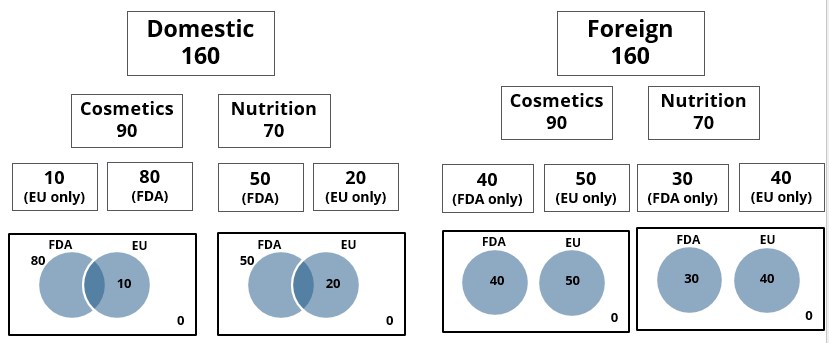
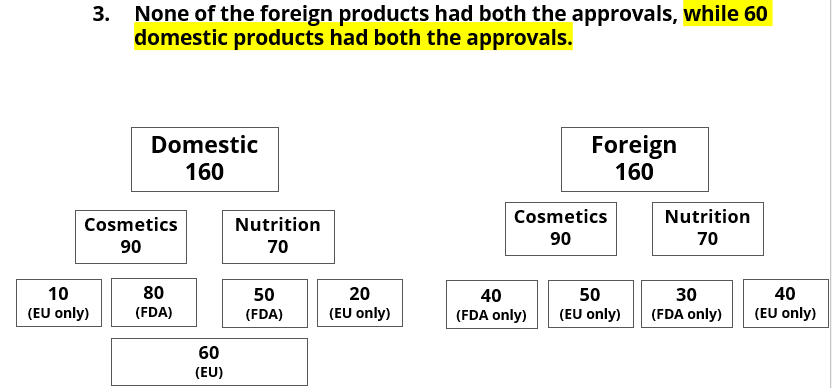
3. None of the foreign products had both the approvals, while 60 domestic products had both the approvals.
4. There were 140 nutrition products, half of them were foreign products.
5. There were 200 FDA approved products. 70 of them were foreign products and 120 of them were cosmetic products.
How many foreign products were FDA approved cosmetic products?
Video Explanation

Explanatory Answer
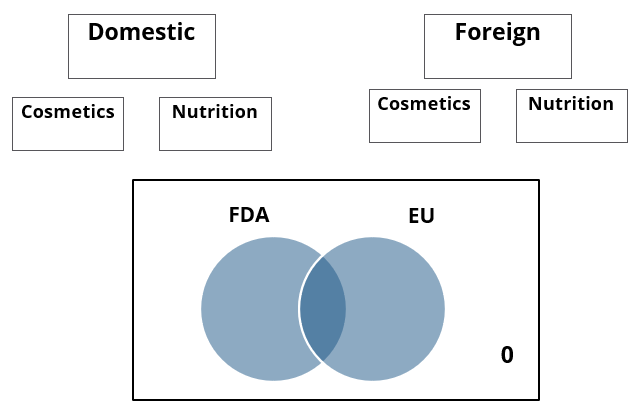

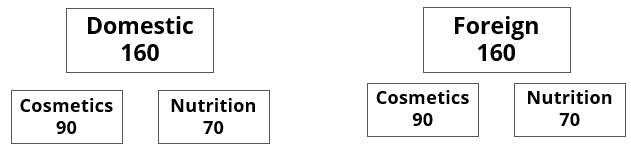

How many cosmetic products did not have FDA approval?
Video Explanation

Explanatory Answer








Which among the following options best represents the number of domestic cosmetic products that had both the approvals?
Video Explanation

Explanatory Answer








If 70 cosmetic products did not have EU approval, then how many nutrition products had both the approvals?
Video Explanation

Explanatory Answer








If 50 nutrition products did not have EU approval, then how many domestic cosmetic products did not have EU approval?
Video Explanation

Explanatory Answer








How many foreign products were FDA approved cosmetic products?
Video Explanation

Explanatory Answer








How many cosmetic products did not have FDA approval?
Video Explanation

Explanatory Answer








Which among the following options best represents the number of domestic cosmetic products that had both the approvals?
Video Explanation

Explanatory Answer








If 70 cosmetic products did not have EU approval, then how many nutrition products had both the approvals?
Video Explanation

Explanatory Answer








If 50 nutrition products did not have EU approval, then how many domestic cosmetic products did not have EU approval?
Video Explanation

Explanatory Answer








Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.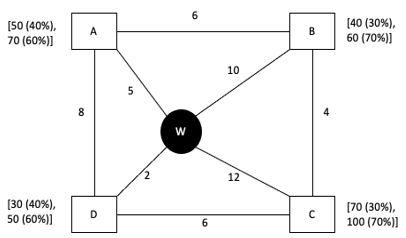
Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
If the last location visited is Ahmednagar, then what is the total distance covered in the route (in km)?
Video Explanation

Explanatory Answer
The question is " If the last location visited is Ahmednagar, then what is the total distance covered in the route (in km)? "
Hence, the answer is '35'
If the total number of widgets delivered in a day is 250 units, then what is the total distance covered in the route (in km)?
Video Explanation

Explanatory Answer
The question is " If the total number of widgets delivered in a day is 250 units, then what is the total distance covered in the route (in km)? "
Hence, the answer is '38'
What is the chance that the total number of widgets delivered in a day is 260 units and the route ends at Bikrampore?
Video Explanation

Explanatory Answer
The question is " What is the chance that the total number of widgets delivered in a day is 260 units and the route ends at Bikrampore? "
Hence, the answer is '7.56%'
Choice C is the correct answer.
If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?
Video Explanation

Explanatory Answer
The question is " If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km? "
Hence, the answer is '18%'
Choice D is the correct answer.
If Ahmednagar is not the first location to be visited in a route and the total route distance is 29 km, then which of the following is a possible number of widgets delivered on that day?
Video Explanation

Explanatory Answer
The question is " If Ahmednagar is not the first location to be visited in a route and the total route distance is 29 km, then which of the following is a possible number of widgets delivered on that day? "
Hence, the answer is '210'
Choice A is the correct answer.
If the last location visited is Ahmednagar, then what is the total distance covered in the route (in km)?
Video Explanation

Explanatory Answer
The question is " If the last location visited is Ahmednagar, then what is the total distance covered in the route (in km)? "
Hence, the answer is '35'
If the total number of widgets delivered in a day is 250 units, then what is the total distance covered in the route (in km)?
Video Explanation

Explanatory Answer
The question is " If the total number of widgets delivered in a day is 250 units, then what is the total distance covered in the route (in km)? "
Hence, the answer is '38'
What is the chance that the total number of widgets delivered in a day is 260 units and the route ends at Bikrampore?
Video Explanation

Explanatory Answer
The question is " What is the chance that the total number of widgets delivered in a day is 260 units and the route ends at Bikrampore? "
Hence, the answer is '7.56%'
Choice C is the correct answer.
If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?
Video Explanation

Explanatory Answer
The question is " If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km? "
Hence, the answer is '18%'
Choice D is the correct answer.
If Ahmednagar is not the first location to be visited in a route and the total route distance is 29 km, then which of the following is a possible number of widgets delivered on that day?
Video Explanation

Explanatory Answer
The question is " If Ahmednagar is not the first location to be visited in a route and the total route distance is 29 km, then which of the following is a possible number of widgets delivered on that day? "
Hence, the answer is '210'
Choice A is the correct answer.
How many households did Lahur meet on the second day?
Video Explanation

Explanatory Answer
1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.
2. On both days, Lahur met the same number of households and sold the same number of items.
3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.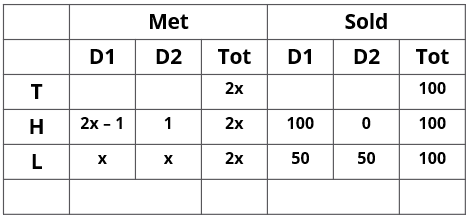
4. Tohri met 30 more households on the second day than on the first day.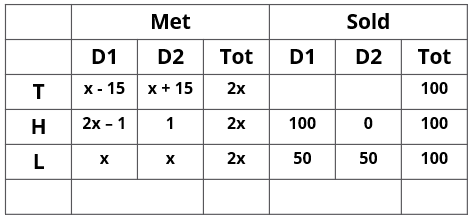
5. Tohri's success rate was twice that of Lahur's on the first day, and it was 75% of Lahur's on the second day.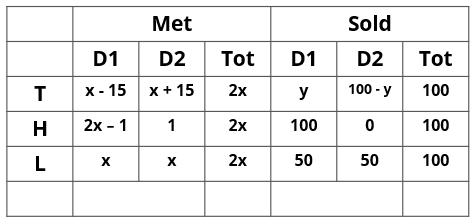
yx−15yx−15 = 50x50x*2
100−yx+15100−yx+15 = 50x50x*3434
xy = 100(x–15).
4x(100–y) = 150(x+15)
400x – 4xy = 150(x+15)
400x – 4*100(x–15) = 150(x+15) 400 * 15 = 150 (x+15). x = 25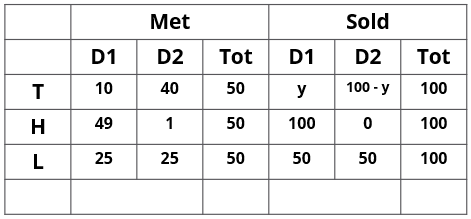
y10y10 = 50255025*2
y = 40
How many households did Tohri meet on the first day?
Video Explanation

Explanatory Answer
1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.

2. On both days, Lahur met the same number of households and sold the same number of items.
3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.
4. Tohri met 30 more households on the second day than on the first day.
5. Tohri's success rate was twice that of Lahur's on the first day, and it was 75% of Lahur's on the second day.
yx−15yx−15 = 50x50x*2
100−yx+15100−yx+15 = 50x50x*3434
xy = 100(x–15).
4x(100–y) = 150(x+15)
400x – 4xy = 150(x+15)
400x – 4*100(x–15) = 150(x+15) 400 * 15 = 150 (x+15). x = 25
y10y10 = 50255025*2
y = 40
Which of the following statements is FALSE?
Video Explanation

Explanatory Answer
1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.

2. On both days, Lahur met the same number of households and sold the same number of items.
3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.
4. Tohri met 30 more households on the second day than on the first day.
5. Tohri's success rate was twice that of Lahur's on the first day, and it was 75% of Lahur's on the second day.
yx−15yx−15 = 50x50x*2
100−yx+15100−yx+15 = 50x50x*3434
xy = 100(x–15).
4x(100–y) = 150(x+15)
400x – 4xy = 150(x+15)
400x – 4*100(x–15) = 150(x+15) 400 * 15 = 150 (x+15). x = 25
y10y10 = 50255025*2
y = 40
A few salesmen are employed to sell a product called TRICCEK among households in various housing complexes. On each day, a salesman is assigned to visit one housing complex. Once a salesman enters a housing complex, he can meet any number of households in the time available. However, if a household makes a complaint against the salesman, then he must leave the housing complex immediately and cannot meet any other household on that day. A household may buy any number of TRICCEK items or may not buy any item. The salesman needs to record the total number of TRICCEK items sold as well as the number of households met in each day. The success rate of a salesman for a day is defined as the ratio of the number of items sold to the number of households met on that day. Some details about the performances of three salesmen - Tohri, Hokli and Lahur, on two particular days are given below.
1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.
2. On both days, Lahur met the same number of households and sold the same number of items.
3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.
4. Tohri met 30 more households on the second day than on the first day.
5. Tohri's success rate was twice that of Lahur's on the first day, and it was 75% of Lahur's on the second day.
What was the total number of households met by Tohri, Hokli and Lahur on the first day?
Video Explanation

Explanatory Answer
1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.

2. On both days, Lahur met the same number of households and sold the same number of items.
3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.
4. Tohri met 30 more households on the second day than on the first day.
5. Tohri's success rate was twice that of Lahur's on the first day, and it was 75% of Lahur's on the second day.
yx−15yx−15 = 50x50x*2
100−yx+15100−yx+15 = 50x50x*3434
xy = 100(x–15).
4x(100–y) = 150(x+15)
400x – 4xy = 150(x+15)
400x – 4*100(x–15) = 150(x+15) 400 * 15 = 150 (x+15). x = 25
y10y10 = 50255025*2
y = 40
How many TRICCEK items were sold by Tohri on the first day?
Video Explanation

Explanatory Answer
1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.

2. On both days, Lahur met the same number of households and sold the same number of items.
3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.
4. Tohri met 30 more households on the second day than on the first day.
5. Tohri's success rate was twice that of Lahur's on the first day, and it was 75% of Lahur's on the second day.
yx−15yx−15 = 50x50x*2
100−yx+15100−yx+15 = 50x50x*3434
xy = 100(x–15).
4x(100–y) = 150(x+15)
400x – 4xy = 150(x+15)
400x – 4*100(x–15) = 150(x+15) 400 * 15 = 150 (x+15). x = 25
y10y10 = 50255025*2
y = 40
How many households did Lahur meet on the second day?
Video Explanation

Explanatory Answer
1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.

2. On both days, Lahur met the same number of households and sold the same number of items.
3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.
4. Tohri met 30 more households on the second day than on the first day.
5. Tohri's success rate was twice that of Lahur's on the first day, and it was 75% of Lahur's on the second day.
yx−15yx−15 = 50x50x*2
100−yx+15100−yx+15 = 50x50x*3434
xy = 100(x–15).
4x(100–y) = 150(x+15)
400x – 4xy = 150(x+15)
400x – 4*100(x–15) = 150(x+15) 400 * 15 = 150 (x+15). x = 25
y10y10 = 50255025*2
y = 40
How many households did Tohri meet on the first day?
Video Explanation

Explanatory Answer
1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.

2. On both days, Lahur met the same number of households and sold the same number of items.
3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.
4. Tohri met 30 more households on the second day than on the first day.
5. Tohri's success rate was twice that of Lahur's on the first day, and it was 75% of Lahur's on the second day.
yx−15yx−15 = 50x50x*2
100−yx+15100−yx+15 = 50x50x*3434
xy = 100(x–15).
4x(100–y) = 150(x+15)
400x – 4xy = 150(x+15)
400x – 4*100(x–15) = 150(x+15) 400 * 15 = 150 (x+15). x = 25
y10y10 = 50255025*2
y = 40
Which of the following statements is FALSE?
Video Explanation

Explanatory Answer
1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.

2. On both days, Lahur met the same number of households and sold the same number of items.
3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.
4. Tohri met 30 more households on the second day than on the first day.
5. Tohri's success rate was twice that of Lahur's on the first day, and it was 75% of Lahur's on the second day.
yx−15yx−15 = 50x50x*2
100−yx+15100−yx+15 = 50x50x*3434
xy = 100(x–15).
4x(100–y) = 150(x+15)
400x – 4xy = 150(x+15)
400x – 4*100(x–15) = 150(x+15) 400 * 15 = 150 (x+15). x = 25
y10y10 = 50255025*2
y = 40
What was the total number of households met by Tohri, Hokli and Lahur on the first day?
Video Explanation

Explanatory Answer
1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.

2. On both days, Lahur met the same number of households and sold the same number of items.
3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.
4. Tohri met 30 more households on the second day than on the first day.
5. Tohri's success rate was twice that of Lahur's on the first day, and it was 75% of Lahur's on the second day.
yx−15yx−15 = 50x50x*2
100−yx+15100−yx+15 = 50x50x*3434
xy = 100(x–15).
4x(100–y) = 150(x+15)
400x – 4xy = 150(x+15)
400x – 4*100(x–15) = 150(x+15) 400 * 15 = 150 (x+15). x = 25
y10y10 = 50255025*2
y = 40
How many TRICCEK items were sold by Tohri on the first day?
Video Explanation

Explanatory Answer
1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.

2. On both days, Lahur met the same number of households and sold the same number of items.
3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.
4. Tohri met 30 more households on the second day than on the first day.
5. Tohri's success rate was twice that of Lahur's on the first day, and it was 75% of Lahur's on the second day.
yx−15yx−15 = 50x50x*2
100−yx+15100−yx+15 = 50x50x*3434
xy = 100(x–15).
4x(100–y) = 150(x+15)
400x – 4xy = 150(x+15)
400x – 4*100(x–15) = 150(x+15) 400 * 15 = 150 (x+15). x = 25
y10y10 = 50255025*2
y = 40
The price of a precious stone is directly proportional to the square of its weight. Sita has a precious stone weighing 18 units. If she breaks it into four pieces with each piece having distinct integer weight, then the difference between the highest and lowest possible values of the total price of the four pieces will be 288000. Then, the price of the original precious stone is
Video Explanation

Explanatory Answer

Anil borrows Rs 2 lakhs at an interest rate of 8% per annum, compounded half-yearly. He repays Rs 10320 at the end of the first year and closes the loan by paying the outstanding amount at the end of the third year. Then, the total interest, in rupees, paid over the three years is nearest to
Video Explanation

Explanatory Answer

Ravi is driving at a speed of 40 km/h on a road. Vijay is 54 meters behind Ravi and driving in the same direction as Ravi. Ashok is driving along the same road from the opposite direction at a speed of 50 km/h and is 225 meters away from Ravi. The speed, in km/h, at which Vijay should drive so that all the three cross each other at the same time, is
Video Explanation

Explanatory Answer
The speeds of Ravi and Ashok converted to meters per second are 40×5/18=100/9 m/s and 50×5/18=1259 m/s50×518=125/9 m/s respectively.
The relative speed between Ravi and Ashok = 100/9+125/9=225/9 m/s
So they meet exactly after 225/225/9=9 seconds.The distance covered by R in 9 seconds = 100/9×9=100 m.
So, for all three of them to meet at the same time Vijay has to cover 54 + 100 = 154m in 9
Seconds.
∴ The speed of Vijay = 154/9 m/s=154/9×185=61.6kmph
Pipes A and C are fill pipes while Pipe B is a drain pipe of a tank. Pipe B empties the full tank in one hour less than the time taken by Pipe A to fill the empty tank. When pipes A, B and C are turned on together, the empty tank is filled in two hours. If pipes B and C are turned on together when the tank is empty and Pipe B is turned off after one hour, then Pipe C takes another one hour and 15 minutes to fill the remaining tank. If Pipe A can fill the empty tank in less than five hours, then the time taken, in minutes, by Pipe C to fill the empty tank is
Video Explanation

Explanatory Answer
Let the time taken by A to fill the tank alone be x hr, which implies the time taken by B to empty the tank alone is (x-1)hr B is the drainage pipe, and the time taken by C to fill the tank is y hours
It is given that when pipe A,B and C are turned on together, the empty tank is filled in two hours. Hence, 1/x- 1/x-1 +1/y= 1/2
It is given that if pipes B and C are turned on together when the tank is empty and pipe B is turned off after one hour, then pipe C takes another one hour and 15 min to fill the remaining tank
Hence, B worked for 1hr, and C worked for 2hr 15min, which is equal to 9/4hours
In 1 hour, B worked -1/x-1 units, and in 9/4 hours, C worked 9/4y units. Hence, 9/4y-1/x-1=1
Solving both the equations we get y=3/2 and x=3. Hence, the time taken by C is 3/2 hr which is equal to 90 Min
Minu purchases a pair of sunglasses at Rs.1000 and sells to Kanu at 20% profit. Then, Kanu sells it back to Minu at 20% loss. Finally, Minu sells the same pair of sunglasses to Tanu. If the total profit made by Minu from all her transactions is Rs.500, then the percentage of profit made by Minu when she sold the pair of sunglasses to Tanu is
Video Explanation

Explanatory Answer
“Minu purchases a pair of sunglasses at Rs.1000 and sells to Kanu at 20% profit.”
This means, Minu purchased the glasses at Rs.1000 and sold them to Kanu at Rs.1200.
Minu made a profit of Rs. 200 so far.
“Then, Kanu sells it back to Minu at 20% loss.”
This means, Kanu sold the glasses back to Minu at 80% of 1200 = Rs. 960
“Finally, Minu sells the same pair of sunglasses to Tanu the total profit made by Minu from all her transactions is Rs.500”
This means, Minu has to make a further profit of Rs. 300. She achieves this by selling the glasses back to Tanu at 960 + 300 = Rs.1260
So the profit % in the transaction is 300/960×100=31.25%
In a company, 20% of the employees work in the manufacturing department. If the total salary obtained by all the manufacturing employees is one-sixth of the total salary obtained by all the employees in the company, then the ratio of the average salary obtained by the manufacturing employees to the average salary obtained by the non-manufacturing employees is
Video Explanation

Explanatory Answer
In a company, 20% of the employees work in the manufacturing department.” The ratio of number of manufacturing to non-manufacturing employees = 1: 4
So, let the number of manufacturing to non-manufacturing employees be x and 4x respectively. “the total salary obtained by all the manufacturing employees is one-sixth of the total salary obtained by all the employees in the company,” Ratio of total salaries of manufacturing to non-manufacturing employees = 1: 5
So, let the total salaries of manufacturing to non-manufacturing employees be y and 5y respectively.
So, the ratio of average salaries of manufacturing to non-manufacturing employees will be y/x:5y/ 4x=4:5
The number of positive integers less than 50, having exactly two distinct factors other than 1 and itself, is
Video Explanation

Explanatory Answer
A positive integer less than 50, having exactly two distinct factors other than 1 and itself, is either a perfect cube below 50 or an integer that is a product of exactly two distinct primes.
Case i)
Perfect cubes below 50 are 23 and 33. So, two numbers here
Case ii)
For the product of two primes to be below 50, the individual primes should be below 25.
(Because, the smallest prime is 2 and multiplying 2 with anything greater than or equal to 25 yields a number greater than or equal to 50.)
2, 3, 5, 7, 11, 13, 17, 19, 23 are prime numbers less than 25.
2, 3, 5, 7 are the primes less than √50, any product of two numbers among them yields a product less than 50.
![]()
11, 13, 17, 19, 23 are the primes greater than √50, any product of two numbers among them yields a product greater than 50.
So, there are 0 pairs here.
Between the two lists 11 and 13 can pair with 2 and 3, while 17, 19, and 23 can only pair with 2.
So, there are 7 pairs here.
So, totally, there are 2 + 6 + 0 + 7 = 15 such numbers.