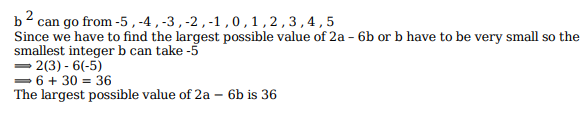Live Updates
• CATKing has launched new chat bot.
• New video on Logs has been released.
495
Learners
asked the doubt
Previous Year Questions
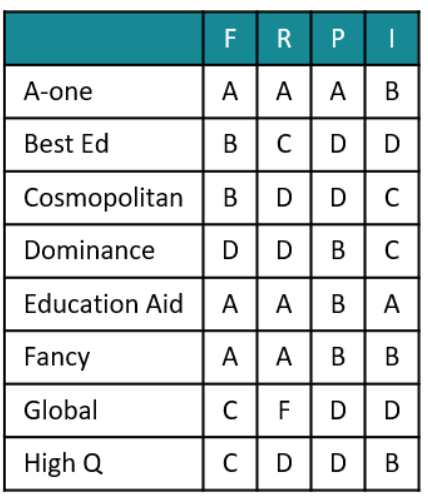
College Accreditation
An agency entrusted to accredit colleges looks at four parameters: faculty quality (F), reputation (R), placement quality (P), and infrastructure (I). The four parameters are used to arrive at an overall score, which the agency uses to give an accreditation to the colleges. In each parameter, there are five possible letter grades given, each carrying certain points: A (50 points), B (40 points), C (30 points), D (20 points), and F (0 points). The overall score for a college is the weighted sum of the points scored in the four parameters. The weights of the parameters are 0.1, 0.2, 0.3 and 0.4 in some order, but the order is not disclosed.
Accreditation is awarded based on the following scheme:
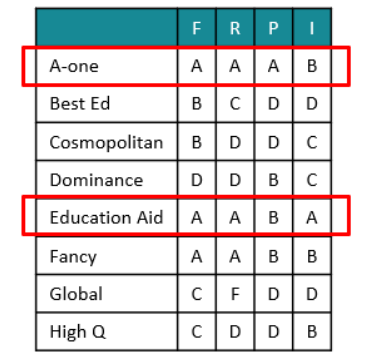
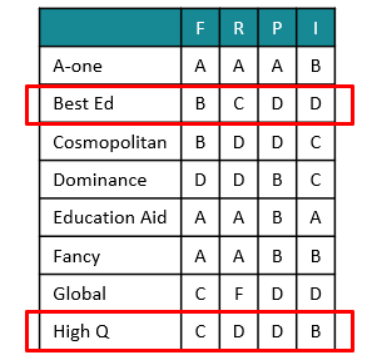
Eight colleges apply for accreditation, and receive the following grades in the four parameters (F, R, P, and I):
It is further known that in terms of overall scores:
1. High Q is better than Best Ed.
2. Best Ed is better than Cosmopolitan.
3. Education Aid is better than A-one.
What is the weight of the faculty quality parameter?
Video Explanation
Explanatory Answer
Let us look at this one at a time. Statement 1 does not give us clear comparables, let us start with
statement 2.
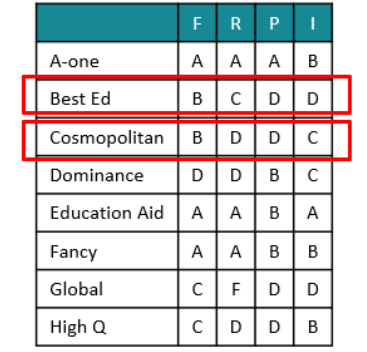
Ratings in F and P are identical, so we can infer that Weightage for R > Weightage for I.
R > I.
Now, let us move to statement 3.
Ratings in F and R are identical, so we can infer that Weightage for I > Weightage for P.
I > P.
Now, let us combine these two inferences – we get R > I > P.
Now, let us look at Statement 1.
Scores in P are identical. Best Ed has gotten better scores in F and R and a worse score in I.
Further Best Ed has gotten better score by one grade in F and R, but worse score by two grades
in I.
So, Best Ed’s better score in two grades is more than offset by High Q’s better score in one
parameter.
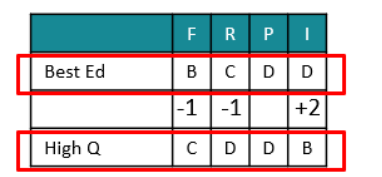
High Q is -1 in F and R, but +2 in I. We know that weightage given for R > I.
So, the -1 in R has a great impact, so the -1 in F should have much lower impact.
In other words, weightage for F should be small and that for I should be high.
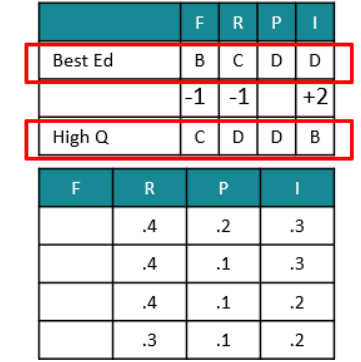
Let us account for R > I > P first.
Of the 4 possibilities, we can easily eliminate the last one as F cannot be 0.4.
F cannot be 0.3 either, so the 3rd one can also be eliminated.
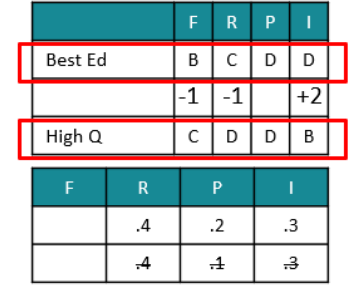
Even if F were 0.2, High Q would not be higher than Best End – the two scores would be equal.
So, the weightages have to be F = 0.1, R = 0.4, P = 0.2 and I = 0.3.
So, the weightages are as follows.
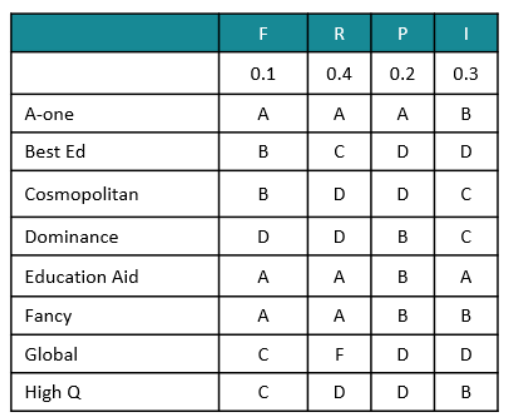
From the above table, we can see that the weight of the faculty quality parameter is 0.1.
How many colleges receive the accreditation of AAA? [TITA]
Video Explanation
Explanatory Answer
Let us look at this one at a time. Statement 1 does not give us clear comparables, let us start with
statement 2.
Ratings in F and P are identical, so we can infer that Weightage for R > Weightage for I.
R > I.
Now, let us move to statement 3.
Ratings in F and R are identical, so we can infer that Weightage for I > Weightage for P.
I > P.
Now, let us combine these two inferences – we get R > I > P.
Now, let us look at Statement 1.
Scores in P are identical. Best Ed has gotten better scores in F and R and a worse score in I.
Further Best Ed has gotten better score by one grade in F and R, but worse score by two grades
in I.
So, Best Ed’s better score in two grades is more than offset by High Q’s better score in one
parameter.
High Q is -1 in F and R, but +2 in I. We know that weightage given for R > I.
So, the -1 in R has a great impact, so the -1 in F should have much lower impact.
In other words, weightage for F should be small and that for I should be high.
Let us account for R > I > P first.
Of the 4 possibilities, we can easily eliminate the last one as F cannot be 0.4.
F cannot be 0.3 either, so the 3rd one can also be eliminated.
Even if F were 0.2, High Q would not be higher than Best End – the two scores would be equal.
So, the weightages have to be F = 0.1, R = 0.4, P = 0.2 and I = 0.3.
So, the weightages are as follows.
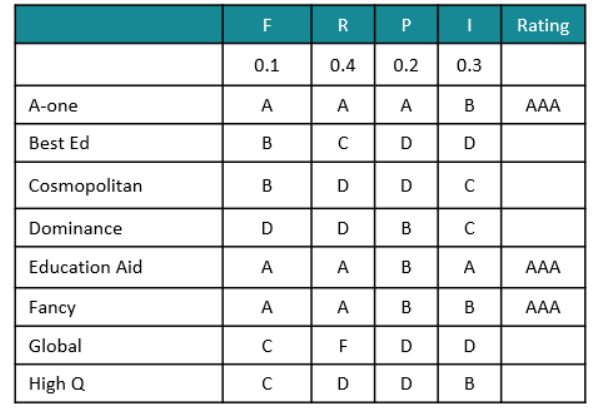
From the above table, we can see that the number of colleges which received AAA accredditation
is 3.
What is the highest overall score among the eight colleges? [TITA]
Video Explanation
Explanatory Answer
Let us look at this one at a time. Statement 1 does not give us clear comparables, let us start with
statement 2.
Ratings in F and P are identical, so we can infer that Weightage for R > Weightage for I.
R > I.
Now, let us move to statement 3.
Ratings in F and R are identical, so we can infer that Weightage for I > Weightage for P.
I > P.
Now, let us combine these two inferences – we get R > I > P.
Now, let us look at Statement 1.
Scores in P are identical. Best Ed has gotten better scores in F and R and a worse score in I.
Further Best Ed has gotten better score by one grade in F and R, but worse score by two grades
in I.
So, Best Ed’s better score in two grades is more than offset by High Q’s better score in one
parameter.
High Q is -1 in F and R, but +2 in I. We know that weightage given for R > I.
So, the -1 in R has a great impact, so the -1 in F should have much lower impact.
In other words, weightage for F should be small and that for I should be high.
Let us account for R > I > P first.
Of the 4 possibilities, we can easily eliminate the last one as F cannot be 0.4.
F cannot be 0.3 either, so the 3rd one can also be eliminated.
Even if F were 0.2, High Q would not be higher than Best End – the two scores would be equal.
So, the weightages have to be F = 0.1, R = 0.4, P = 0.2 and I = 0.3.
So, the weightages are as follows.
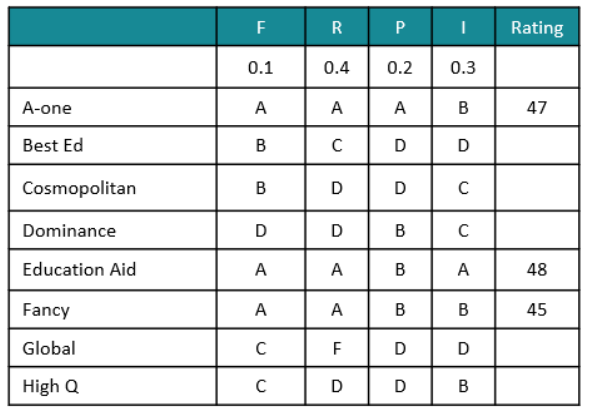
From the above table, we can see that the highest overall score among the eight colleges is 48.
How many colleges have overall scores between 31 and 40, both inclusive?
Video Explanation
Explanatory Answer
Let us look at this one at a time. Statement 1 does not give us clear comparables, let us start with
statement 2.
Ratings in F and P are identical, so we can infer that Weightage for R > Weightage for I.
R > I.
Now, let us move to statement 3.
Ratings in F and R are identical, so we can infer that Weightage for I > Weightage for P.
I > P.
Now, let us combine these two inferences – we get R > I > P.
Now, let us look at Statement 1.
Scores in P are identical. Best Ed has gotten better scores in F and R and a worse score in I.
Further Best Ed has gotten better score by one grade in F and R, but worse score by two grades
in I.
So, Best Ed’s better score in two grades is more than offset by High Q’s better score in one
parameter.
High Q is -1 in F and R, but +2 in I. We know that weightage given for R > I.
So, the -1 in R has a great impact, so the -1 in F should have much lower impact.
In other words, weightage for F should be small and that for I should be high.
Let us account for R > I > P first.
Of the 4 possibilities, we can easily eliminate the last one as F cannot be 0.4.
F cannot be 0.3 either, so the 3rd one can also be eliminated.
Even if F were 0.2, High Q would not be higher than Best End – the two scores would be equal.
So, the weightages have to be F = 0.1, R = 0.4, P = 0.2 and I = 0.3.
So, the weightages are as follows.
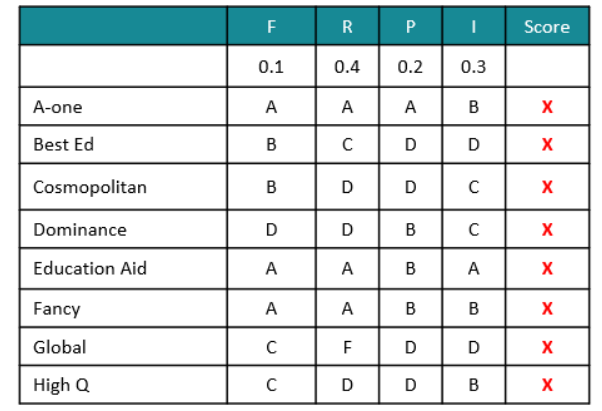
From the above table, we can see that the number of colleges which have overall scores between
31 and 40 both inclusive is 0.
What is the weight of the faculty quality parameter?
Video Explanation
Explanatory Answer
Let us look at this one at a time. Statement 1 does not give us clear comparables, let us start with
statement 2.
Ratings in F and P are identical, so we can infer that Weightage for R > Weightage for I.
R > I.
Now, let us move to statement 3.
Ratings in F and R are identical, so we can infer that Weightage for I > Weightage for P.
I > P.
Now, let us combine these two inferences – we get R > I > P.
Now, let us look at Statement 1.
Scores in P are identical. Best Ed has gotten better scores in F and R and a worse score in I.
Further Best Ed has gotten better score by one grade in F and R, but worse score by two grades
in I.
So, Best Ed’s better score in two grades is more than offset by High Q’s better score in one
parameter.
High Q is -1 in F and R, but +2 in I. We know that weightage given for R > I.
So, the -1 in R has a great impact, so the -1 in F should have much lower impact.
In other words, weightage for F should be small and that for I should be high.
Let us account for R > I > P first.
Of the 4 possibilities, we can easily eliminate the last one as F cannot be 0.4.
F cannot be 0.3 either, so the 3rd one can also be eliminated.
Even if F were 0.2, High Q would not be higher than Best End – the two scores would be equal.
So, the weightages have to be F = 0.1, R = 0.4, P = 0.2 and I = 0.3.
So, the weightages are as follows.
From the above table, we can see that the weight of the faculty quality parameter is 0.1.
How many colleges receive the accreditation of AAA? [TITA]
Video Explanation
Explanatory Answer
Let us look at this one at a time. Statement 1 does not give us clear comparables, let us start with
statement 2.
Ratings in F and P are identical, so we can infer that Weightage for R > Weightage for I.
R > I.
Now, let us move to statement 3.
Ratings in F and R are identical, so we can infer that Weightage for I > Weightage for P.
I > P.
Now, let us combine these two inferences – we get R > I > P.
Now, let us look at Statement 1.
Scores in P are identical. Best Ed has gotten better scores in F and R and a worse score in I.
Further Best Ed has gotten better score by one grade in F and R, but worse score by two grades
in I.
So, Best Ed’s better score in two grades is more than offset by High Q’s better score in one
parameter.
High Q is -1 in F and R, but +2 in I. We know that weightage given for R > I.
So, the -1 in R has a great impact, so the -1 in F should have much lower impact.
In other words, weightage for F should be small and that for I should be high.
Let us account for R > I > P first.
Of the 4 possibilities, we can easily eliminate the last one as F cannot be 0.4.
F cannot be 0.3 either, so the 3rd one can also be eliminated.
Even if F were 0.2, High Q would not be higher than Best End – the two scores would be equal.
So, the weightages have to be F = 0.1, R = 0.4, P = 0.2 and I = 0.3.
So, the weightages are as follows.
From the above table, we can see that the number of colleges which received AAA accredditation
is 3.
What is the minimum possible number of different types of prizes? ?
Video Explanation
What is the maximum possible number of different types of prizes?
Video Explanation
You ask for the type of item in box 45. Instead of being given a direct answer, you are told that there are 31 items of the same type as box 45 in boxes 1 to 44 and 43 items of the same type as box 45 in boxes 46 to 100. What is the maximum possible number of different types of items?
Video Explanation
A new game show on TV has 100 boxes numbered 1, 2, ....., 100 in a row, each containing a mystery prize. The prizes are items of different types, a, b, c, ....., in decreasing order of value. The most expensive item is of type a, a diamond ring, and there is exactly one of these. You are told that the number of items at least doubles as you move to the next type. For example, there would be at least twice as many items of type b as of type a, at least twice as many items of type c as of type b and so on. There is no particular order in which the prizes are placed in the boxes
What is the minimum possible number of different types of prizes? ?
Video Explanation
What is the maximum possible number of different types of prizes?
Video Explanation
You ask for the type of item in box 45. Instead of being given a direct answer, you are told that there are 31 items of the same type as box 45 in boxes 1 to 44 and 43 items of the same type as box 45 in boxes 46 to 100. What is the maximum possible number of different types of items?
Video Explanation
Ramesh and Gautam are among 22 students who write an examination. Ramesh scores 82.5. The average score of the 21 students other than Gautam is 62. The average score of all the 22 students is one more than the average score of the 21 students other than Ramesh. The score of Gautam is
Video Explanation
Explanatory Answer
Consider a function f(x+y) = f(x) f(y) where x , y are positive integers, and f(1) = 2. If f (a+1) + f (a+2) + . + f(a+n) = 16 (2n - 1) then a is equal to
Video Explanation
Explanatory Answer
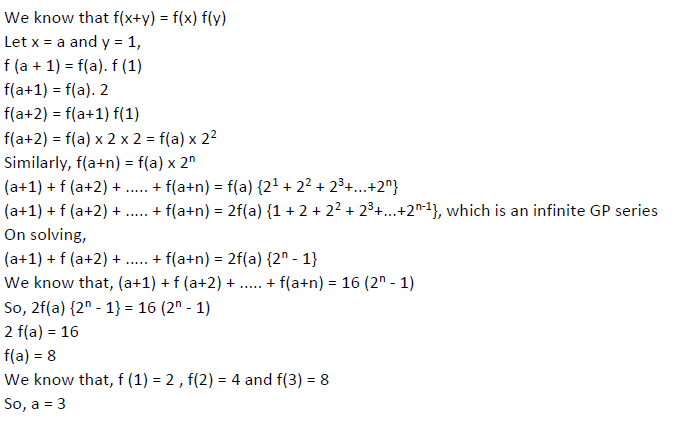
The wheels of bicycles A and B have radii 30 cm and 40 cm, respectively. While traveling a certain distance, each wheel of A required 5000 more revolutions than each wheel of B. If bicycle B traveled this distance in 45 minutes, then its speed, in km per hour, was
Video Explanation
Explanatory Answer
The product of the distinct roots of |x2 - x - 6| = x + 2 is
Video Explanation
Explanatory Answer
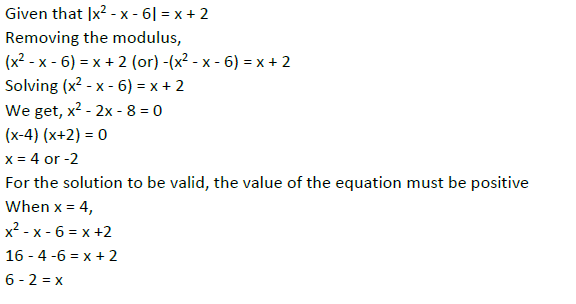
The number of solutions of the equation |x|(6x2 + 1) = 5x2 is
Video Explanation
Explanatory Answer
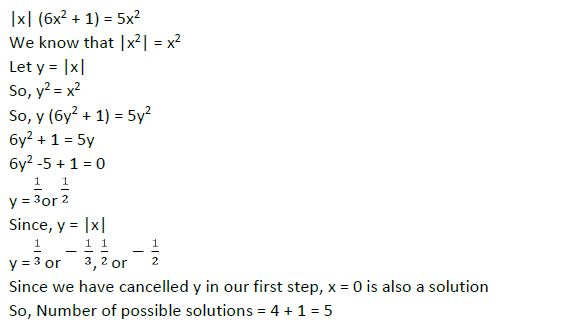
Let S be the set of all points (x,y) in the x-y plane such that |x| + |y| ≤ 2 and |x| ≥ 1. Then, the area, in square units, of the region represented by S equals
Video Explanation
Explanatory Answer
Video Explanation
Explanatory Answer
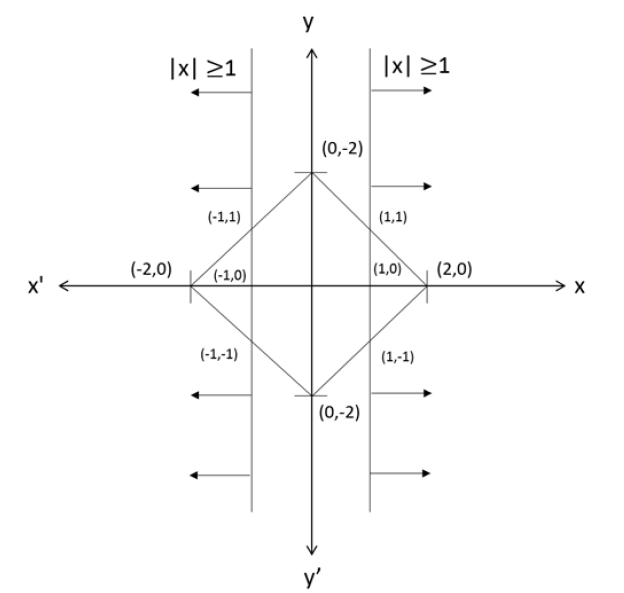
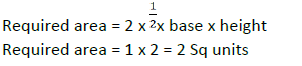
Let x and y be positive real numbers such that log5(x + y) + log5(x - y) = 3, and log2y - log2x = 1 - log23. Then xy equals
Video Explanation
Explanatory Answer
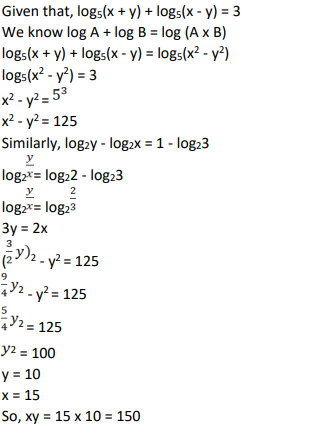
A chemist mixes two liquids 1 and 2. One litre of liquid 1 weighs 1 kg and one litre of liquid 2 weighs 800 gm. If half litre of the mixture weighs 480 gm, then the percentage of liquid 1 in the mixture, in terms of volume, is
Video Explanation
Explanatory Answer
Video Explanation
Explanatory Answer
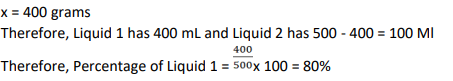
Amala, Bina, and Gouri invest money in the ratio 3 : 4 : 5 in fixed deposits having respective annual interest rates in the ratio 6 : 5 : 4. What is their total interest income (in Rs) after a year, if Bina's interest income exceeds Amala's by Rs 250?
Video Explanation
Explanatory Answer
One can use three different transports which move at 10, 20, and 30 kmph, respectively. To reach from A to B, Amal took each mode of transport 1/3 of his total journey time, while Bimal took each mode of transport 1/3 of the total distance. The percentage by which Bimal's travel time exceeds Amal's travel time is nearest to
Video Explanation
Explanatory Answer
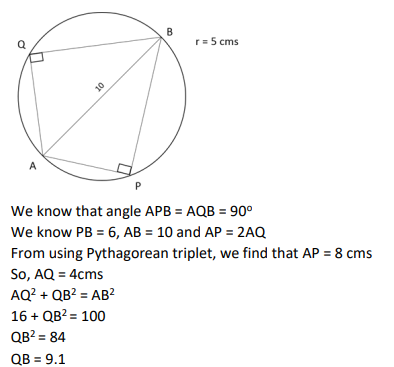
AB is a diameter of a circle of radius 5 cm. Let P and Q be two points on the circle so that the length of PB is 6 cm, and the length of AP is twice that of AQ. Then the length, in cm, of QB is nearest to
Video Explanation
Explanatory Answer
Video Explanation
Explanatory Answer
What was the approximate difference in profit percentages of the store in 2017 and 2018?
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
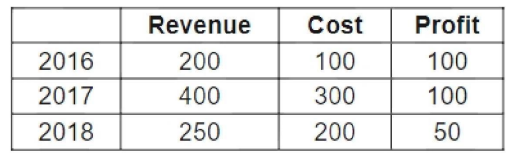
We have the following values for Revenue and cost for the different years
Profit percentage of the store in 2017 =100 /300 =33.3%
Profit percentage of the store in 2018 = 50/200 = 25.0%
The required difference 33.3- 25.0 8.3
Revenue & Cost
A large store has only three departments, Clothing, Produce, and Electronics. The following figure shows the percentages of revenue and cost from the three departments for the years 2016, 2017 and 2018. The dotted lines depict percentage levels. So for example, in 2016, 50% of store's revenue came from its Electronics department while 40% of its costs were incurred in the Produce department.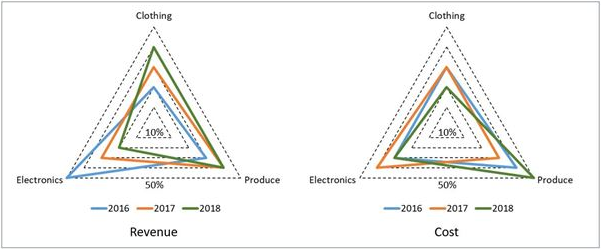
In this setup, Profit is computed as (Revenue – Cost) and Percentage Profit as Profit/Cost × 100%.
It is known that
1. The percentage profit for the store in 2016 was 100%.
2. The store’s revenue doubled from 2016 to 2017, and its cost doubled from 2016 to 2018.
3. There was no profit from the Electronics department in 2017.
4. In 2018, the revenue from the Clothing department was the same as the cost incurred in the Produce department.
What was the percentage profit of the store in 2018? [TITA]
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
We have the following values for Revenue and cost for the different years
Percentage profit of the store in 2018= 50/200 = 25%
What was the ratio of revenue generated from the Produce department In 2017 to that in 2018?
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
We have the following values for Revenue and cost for the different years
The ratio of the revenues =160 :100 = 8 :5
What percentage of the total profits for the store in 2016 was from the Electronics department? [TITA]
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
We have the following values for Revenue and cost for the different years
Profit of the store from the Electronics department in 2016 =100 -30 = 70
Total profit =100 The required percentage = 70%.
What was the approximate difference in profit percentages of the store in 2017 and 2018?
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
We have the following values for Revenue and cost for the different years
Profit percentage of the store in 2017 =100 /300 =33.3%
Profit percentage of the store in 2018 = 50/200 = 25.0%
The required difference 33.3- 25.0 8.3
What was the percentage profit of the store in 2018? [TITA]
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
We have the following values for Revenue and cost for the different years
Percentage profit of the store in 2018= 50/200 = 25%
What was the ratio of revenue generated from the Produce department In 2017 to that in 2018?
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
We have the following values for Revenue and cost for the different years
The ratio of the revenues =160 :100 = 8 :5
What percentage of the total profits for the store in 2016 was from the Electronics department? [TITA]
Video Explanation
Explanatory Answer
The percentage share in Revenue and cost in the different years are as follows
Assume the cost of the store in 2016 to be 100.
As the profit percentage that year was 100, the revenue of the store in that year would be
200 .
Revenue in 2017 would be 400 and cost of the store in 2018 would be 200 . Given that in
2017,30% of 400 = 40% of cost.
120 = 40% of cost or cost in 2017=300
In 2018,50% of 200 = 40% of Revenue
Revenue in 2018 100/0.4= 250
We have the following values for Revenue and cost for the different years
Profit of the store from the Electronics department in 2016 =100 -30 = 70
Total profit =100 The required percentage = 70%.
MT & ET
The first year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common endterm (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions. Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15-mark questions followed the 10-mark questions.
The following additional facts are known.
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
iv. Chetan prepared the third question in both MT and ET; and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
The second question in ET was prepared by:
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
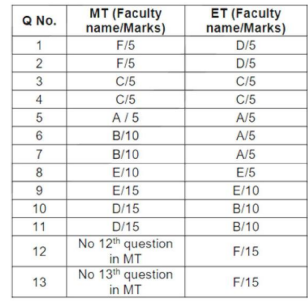
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
How many 5‐mark questions were there in MT and ET combined?
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
Who prepared 15-mark questions for MT and ET?
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
Which of the following questions did Beti prepare in ET?
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
The second question in ET was prepared by:
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
How many 5‐mark questions were there in MT and ET combined?
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
Who prepared 15-mark questions for MT and ET?
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
Which of the following questions did Beti prepare in ET?
Video Explanation
Explanatory Answer
In the following the names of the faculties are referred by first letter of their names.
Given that each of MT and ET carries 100 marks. Each of MT and ET has at least four
questions of 5 marks (4 x 5 = 20), at least three questions of 10 marks (3 x 10 =30) and at
least two questions of 15 marks (2 x 15 = 30). These together add up to 80 marks. The
remaining 20 marks can be of the following possible combinations. (Four questions of 5
marks) or (two questions of 10 marks) or (one question of 5 marks and 1question of 15
marks)or (two questions of five marks and one question of ten marks). Hence, the total
number of questions in MT or ET can be 11 or 12 or 13. It is given that ET has more number
of questions than in MT. Hence, MT has 11 or 12 questions.
It is given that the number of questions given by any faculty in both MT and ET together is
the same. If MT has 12 questions and ET has 13 questions, or if MT has 11 questions and ET
has 12 questions, this condition cannot be satisfied. Hence, MT has 11 (Five 5 marks, three
10 marks and three 15 marks) questions and ET has 13 questions (eight 5 marks, three ten
marks and two 15 marks). This implies, each faculty has given four questions in MT and ET
together. Since it is given that faculty A has given only one question in MT and each of the
other faculties has given more than one question, each of the faculties B, C, D, E and F has
given two questions in MT. This implies faculty A has given three questions in ET and all
other faculties have given two questions each in ET. From the given data we get the
following.
Except A, every other faculty gave at least two questions for MT and all the questions of a
faculty appeared consecutively. Hence, 2nd question in MT is given by F, 4th by C, 10th by D. B
also has given two questions and both appeared consecutively. Hence, 6th and 7th questions
are given by B and the 9th question is given by E. In each test first all 5 marks questions
appeared followed by 10 marks questions and then 15 marks questions. It can be
understood that MT has five 5 marks, three 10 marks and three 15 marks. Hence, in MT
questions 1 to 5 carry 5 marks each, 6 to 8 carry 10 marks each and 9 to 11 carry 15 marks
each.
It can be understood that A has given three questions for ET and each of the others has given two questions. Hence, the 2nd question of ET is given by D, the 4th question by C,
6th and 7th questions by A, 9th by E, 10th and 11th by B and 12th by F. Since ET has eight 5
marks questions, three ten marks questions and two 15 marks questions, questions 1 to 8 of
ET carry 8 marks each, 9 to 11 carry ten marks each, 12 and 13 carry 15 marks each. Thus,
we get the following:
How many pouches contain exactly one coin? [TITA]
Video Explanation
Explanatory Answer
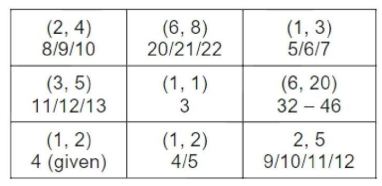
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
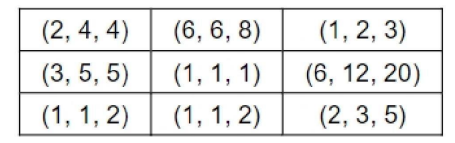
What is the number of slots for which the average amount (in rupees) of its three pouches is an integer? [TITA]
Video Explanation
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
The number of slots for which the total amount in its three pouches strictly exceeds Rs. 10 is [TITA]
Video Explanation
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
In three slots (row 2 , column 1), (row 1 , column 2) and (row 2, column 3), the amount in
the three pouches strictly exceeds 10
Three pouches
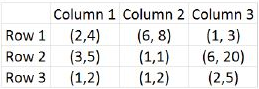
Three pouches (each represented by a filled circle) are kept in each of the nine slots in a 3 × 3 grid, as shown in the figure. Every pouch has a certain number of one-rupee coins. The minimum and maximum amounts of money (in rupees) among the three pouches in each of the nine slots are given in the table. For example, we know that among the three pouches kept in the second column of the first row, the minimum amount in a pouch is Rs. 6 and the maximum amount is Rs. 8.
There are nine pouches in any of the three columns, as well as in any of the three rows. It is known that the average amount of money (in rupees) kept in the nine pouches in any column or in any row is an integer. It is also known that the total amount of money kept in the three pouches in the first column of the third row is Rs. 4.
What is the total amount of money (in rupees) in the three pouches kept in the first column of the second row? [TITA]
Video Explanation
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
How many pouches contain exactly one coin? [TITA]
Video Explanation
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
What is the number of slots for which the average amount (in rupees) of its three pouches is an integer? [TITA]
Video Explanation
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
The number of slots for which the total amount in its three pouches strictly exceeds Rs. 10 is [TITA]
Video Explanation
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
In three slots (row 2 , column 1), (row 1 , column 2) and (row 2, column 3), the amount in
the three pouches strictly exceeds 10
What is the total amount of money (in rupees) in the three pouches kept in the first column of the second row? [TITA]
Video Explanation
Explanatory Answer
The minimum and maximum and possible number of coins (overall) in each slot would be as
follows:
It is given that the average amount of money kept in the nine pouches in any column or any
row is an integer (a multiple of nine).
The total amount of money in the first column must be either 18 or 27 . The minimum value
of the sum of money in the three slots is 8 11 4 23 and the maximum value is
10+13+ 4 = 27.
The number of coins in the first column of the three rows are 10(2 + 4 + 4),13(3+ 5 + 5)
and 4(1+ 2 +1) Similarly in the third row, the sum must be 18 and in the second column, the
sum must be 27.
The number of coins in the second column is 20(6+6 + 8) + 3(1+1+1) and 4(1+1+ 2)
The third column in the first row would be 6(1+ 2 + 3) and the third column in the third row
would be 10(2 + 3 +5)
In the last column, the value in the second row would be 54 -16 = 38(6 +12 +20)
We have the following figure for the number of coins in the pouches in each slot
Video Explanation
Explanatory Answer
The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. If three salt solutions A, B, C are mixed in the proportion 1 : 2 : 3, then the resulting solution has strength 20%. If instead the proportion is 3 : 2 : 1, then the resulting solution has strength 30%. A fourth solution, D, is produced by mixing B and C in the ratio 2 : 7. The ratio of the strength of D to that of A is
Video Explanation
If A = {62n - 35n - 1: n = 1,2,3,.} and B = {35(n-1) : n = 1,2,3,.} then which of the following is true?
Video Explanation
Explanatory Answer
For two sets A and B, let AΔB denote the set of elements which belong to A or B but not both. If P = {1,2,3,4}, Q = {2,3,5,6,}, R = {1,3,7,8,9}, S = {2,4,9,10}, then the number of elements in (PΔQ)Δ(RΔS) is
Video Explanation
Explanatory Answer
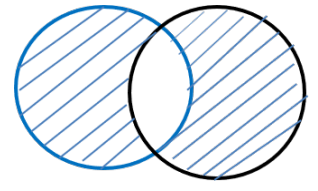
Given that for two sets A and B, A △ B denote the set of elements which belong to A or B but not
both.
This is the diagram which represents A △ B ,the set of elements which belongs to A or B i.e. A
intersection B subtracted from A union B
We have to find the number of elements in (P △ Q) △ (R △ S) if
P = {1 , 2 , 3 , 4} Q = {2 , 3 , 5 , 6 ,} R = {1 , 3 , 7 , 8 , 9} S = {2 , 4 , 9 , 10}
For P △ Q, we have to find the elements which do not to belong to both P and Q such that
(P △ Q) = {1, 4 , 5 , 6}
(R △ S) = {1 , 2 , 3 , 4 , 7 , 8 , 10}
(P △ Q) △ (R △ S) = {2 , 3 , 5 , 7 , 6 , 8 , 10}
The number of elements (P △ Q) △ (R △ S) is 7
Let f(x)=max{5x, 52 - 2x2}, where x is any positive real number.Then the minimum possible value of f(x) is
Video Explanation
Explanatory Answer
Video Explanation
Gopal borrows Rs. X from Ankit at 8% annual interest. He then adds Rs. Y of his own money and lends Rs. X+Y to Ishan at 10% annual interest. At the end of the year, after returning Ankit’s dues, the net interest retained by Gopal is the same as that accrued to Ankit. On the other hand, had Gopal lent Rs. X+2Y to Ishan at 10%, then the net interest retained by him would have increased by Rs. 150. If all interests are compounded annually, then find the value of X + Y.
Video Explanation
Explanatory Answer
Let us draw a flow diagram to understand the transaction
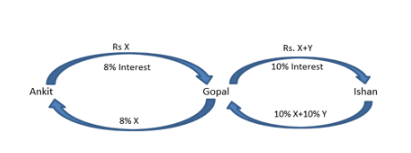
Gopal receives 10% of X + Y from Ishan as interest, from which he pays the interest of 8% of X to
Ankit
So, Gopal would gain 2% of X + 10% of Y as interest and Ankit would gain 8% Interest
Its given that both the interest values are same, so 2% X + 10% Y = 8% X
3% X = 5% Y --- (1)
Its also given that, if Gopal lend Rs. X + 2Y to Ishan at 10% interest, the net interest retained
would increase by Rs. 150
So, the increase in 10% Y accounts for Rs. 150
10% Y = 150 => Y = Rs. 1500
Substituting the value in (1), we get 5 × 1500 = 3 × X => X = 2500
So, X + Y = 2500 + 1500 = Rs 4000
How many two-digit numbers, with a non-zero digit in the units place, are there which are more than thrice the number formed by interchanging the positions of its digits?
Video Explanation
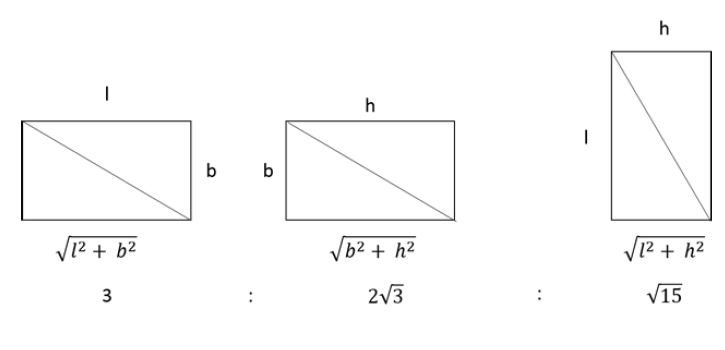
A triangle ABC has area 32 sq units and its side BC, of length 8 units, lies on the line x = 4. Then the shortest possible distance between A and the point (0,0) is
Video Explanation
Explanatory Answer
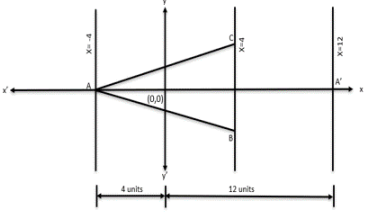
Given Area (△ABC) = 32 sq units and one of the length BC = 8 units on the line x = 4
Let us draw a graph and plot the given values.
We know that area of the Triangle = 1/2 × base × height considering BC as the base,
area of the Triangle = 1/2 × 8 × height = 32
Height = (32×2) / 8 = 64/8 = 8 units
Since the base lies on x = 4 and has a vertical height is of length = 8 units, A can either lie on the
line x = 12 or on x = - 4
However, since we need to find the shortest possible distance between A and the origin, A should
lie on the line x = - 4
So, shortest possible distance to A from the point (0,0) = 4 units
The scores of Amal and Bimal in an examination are in the ratio 11 : 14. After an appeal, their scores increase by the same amount and their new scores are in the ratio 47 : 56. The ratio of Bimal’s new score to that of his original score is
Video Explanation
Explanatory Answer
If a and b are integers such that 2x2 − ax + 2 ＞ 0 and x2 − bx + 8 ≥ 0 for all real numbers x, then the largest possible value of 2a − 6b is
Video Explanation
Explanatory Answer
