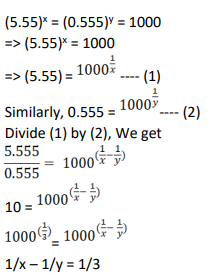Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
495
Learners
asked the doubt

Previous Year Questions
Two types of tea, A and B, are mixed and then sold at Rs. 40 per kg. The profit is 10% if A and B are mixed in the ratio 3 : 2, and 5% if this ratio is 2 : 3. The cost prices, per kg, of A and B are in the ratio
Video Explanation

Explanatory Answer
Let Tea A and B be sold at Rs.a and Rs.b respectively
When A and B are mixed in the ratio 3 : 2 and sold at a profit of 10% at Rs.40 per Kg
3a+2b / 5 = 40/1.1------(1)
When A and B are mixed in the ratio 2 : 3 and sold at a profit of 5% at Rs.40 per Kg
2a+3b/5 = 40/1.05 ------(2)
Solving equations (1) and (2), we get
1.1 × (3a+2b/5) = 1.05 × (2a+3b/5)
11/10 × (3a + 2b) = 21/20 × (2a + 3b)
66a + 44b = 42a + 63b
24a = 19b
a/b = 19/24
So, the cost prices per Kg of A and B are in the ratio 19 : 24
A CAT aspirant appears for a certain number of tests. His average score increases by 1 if the first 10 tests are not considered, and decreases by 1 if the last 10 tests are not considered. If his average scores for the first 10 and the last 10 tests are 20 and 30, respectively, then the total number of tests taken by him is
Video Explanation

Explanatory Answer
Let there be 'n' tests and the Overall Average score be k
Average (n) = k => Total marks = nk
So, when we ignore the first 10 questions,
Average (n-10) = k+1
Similarly, if we ignore the last 10 questions,
Average (first (n-10)) = k-1
It is given that when the first 10 tests are not considered, the overall average increases by 1
(Each question carries 20 marks)
Total marks – 20×10 = (k+1) (n-10)
kn – 200 = (k+1) (n-10) ---(1)
Similarly, If the last 10 tests are not considered, the overall average decreases by 1 (Each
question carries 30 marks)
kn - 300 = (k-1) (n-10) ---(2)
Solving (1) and (2), we get
kn - 200 = (k+1) (n-10)
(-) kn - 300 = (k-1) (n-10)
-------------------------------------
100 = 2(n-10)
50 = n-10
n = 60 questions
The distance from A to B is 60 km. Partha and Narayan start from A at the same time and move towards B. Partha takes four hours more than Narayan to reach B. Moreover, Partha reaches the mid-point of A and B two hours before Narayan reaches B. The speed of Partha, in km per hour, is
Video Explanation

Explanatory Answer
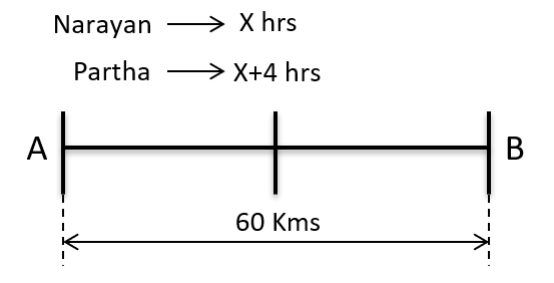
Let Narayanan take X hrs to reach B then Partha would take X + 4 hrs
Its given that Partha reaches the mid-point of A and B two hours before Narayan reaches B
X+4 / 2 = X – 2 => X=8 hrs
So, Partha would take 8+4 = 12 hrs to travel 60 Kms at a speed of 60/12 Kmph
Speed of Partha = 5 Kmph
If f(x + 2) = f(x) + f(x + 1) for all positive integers x, and f(11) = 91, f(15) = 617, then f(10) equals.
Video Explanation

Explanatory Answer
Given, f(x+2) = f(x) + f(x+1) f(11) = 91, f(15) = 617
We get 91 + f(12) = f(13)
Let f(12) be equal to some value ‘a’
So, 91 + a = f(13).
f(12) + f(13) = f(14)
a + 91 + a = f(14)
So, f(14) = 2a + 91 f(13) + f(14) = 617
So, 91 + a + 2a + 91 = 617
3a + 182 = 617
a = 145
Substituting the value of a and f(11), we get
f(10)+ 91 = 145
f(10) = 54
What is the maximum number of patients that the clinic can cater to on any single day?
Video Explanation

Explanatory Answer
. From 9-11: 30, we have 150 minutes. Doctors Ben, Kane and Wayne take 10,15 and 20
minutes respectively for each patient. Therefore Ben, Kane and Wayne can see 150/10=15,
150/15=10 and 150/25=6 respectively. Therefore Ben, Kane and Wayne can see a maximum
of 15,10 and 6 patients respectively every day. Sum =31
The queue is never empty on one particular Saturday. Which of the three doctors would earn the maximum amount in consultation charges on that day?
Video Explanation

Explanatory Answer
Given, on Saturday, the queue is not empty.
=> Each doctor sees the maximum number of patients on a day.
Given Ben, Kane and Wayne charge Rs.100, 200 and 300 respectively.
=> Ben earns 15 (100)= Rs.1500,Kane earns 10(200)
= Rs .2000, Wayne earns 6(300)= Rs .1800
Therefore, Kane earns the maximum amount.
Ans: (Dr. Kane)
Mr. Singh visited the clinic on Monday, Wednesday, and Friday of a particular week, arriving at 8:50 a.m. on each of the three days. His token number was 13 on all three days. On which day was he at the clinic for the maximum duration?
Video Explanation

Explanatory Answer
Mr. Singh takes maximum duration when he enters Dr. Wayne’s room, who sees each
patient for 25 minutes
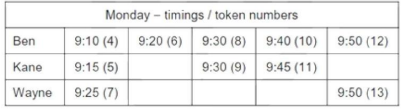
He was at the clinic for 85 minutes.
Similarly On Wednesday, he would meet Ben and he would be at the clinic for 70 minutes.
On Friday, he would meet Ben and he would be at the clinic for 70 minutes.
Therefore, Singh stays at the clinic for the maximum duration on Monday
Ans: (Monday)
On a slow Thursday, only two patients are waiting at 9 a.m. After that two patients keep arriving at exact 15 minute intervals starting at 9:15 a.m. -- i.e. at 9:15 a.m., 9:30 a.m., 9:45 a.m. etc. Then the total duration in minutes when all three doctors are simultaneously free is
Video Explanation

Explanatory Answer
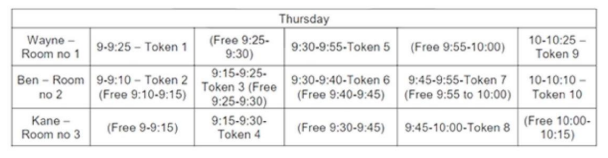
The above pattern continues.
Hence, there is no time where all the doctors are simultaneously free.
Ans: (0)
Three doctors
Three doctors, Dr. Ben, Dr. Kane and Dr. Wayne visit a particular clinic Monday to Saturday to see patients. Dr. Ben sees each patient for 10 minutes and charges Rs. 100/-. Dr. Kane sees each patient for 15 minutes and charges Rs. 200/-, while Dr. Wayne sees each patient for 25 minutes and charges Rs. 300/-. The clinic has three rooms numbered 1, 2 and 3 which are assigned to the three doctors as per the following table.

The clinic is open from 9 a.m. to 11.30 a.m. every Monday to Saturday. On arrival each patient is handed a numbered token indicating their position in the queue, starting with token number 1 every day. As soon as any doctor becomes free, the next patient in the queue enters that emptied room for consultation. If at any time, more than one room is free then the waiting patient enters the room with the smallest number. For example, if the next two patients in the queue have token numbers 7 and 8 and if rooms numbered 1 and 3 are free, then patient with token number 7 enters room number 1 and patient with token number 8 enters room number 3.
What is the maximum number of patients that the clinic can cater to on any single day?
Video Explanation

Explanatory Answer
. From 9-11: 30, we have 150 minutes. Doctors Ben, Kane and Wayne take 10,15 and 20
minutes respectively for each patient. Therefore Ben, Kane and Wayne can see 150/10=15,
150/15=10 and 150/25=6 respectively. Therefore Ben, Kane and Wayne can see a maximum
of 15,10 and 6 patients respectively every day. Sum =31
The queue is never empty on one particular Saturday. Which of the three doctors would earn the maximum amount in consultation charges on that day?
Video Explanation

Explanatory Answer
Given, on Saturday, the queue is not empty.
=> Each doctor sees the maximum number of patients on a day.
Given Ben, Kane and Wayne charge Rs.100, 200 and 300 respectively.
=> Ben earns 15 (100)= Rs.1500,Kane earns 10(200)
= Rs .2000, Wayne earns 6(300)= Rs .1800
Therefore, Kane earns the maximum amount.
Ans: (Dr. Kane)
Mr. Singh visited the clinic on Monday, Wednesday, and Friday of a particular week, arriving at 8:50 a.m. on each of the three days. His token number was 13 on all three days. On which day was he at the clinic for the maximum duration?
Video Explanation

Explanatory Answer
Mr. Singh takes maximum duration when he enters Dr. Wayne’s room, who sees each
patient for 25 minutes

He was at the clinic for 85 minutes.
Similarly On Wednesday, he would meet Ben and he would be at the clinic for 70 minutes.
On Friday, he would meet Ben and he would be at the clinic for 70 minutes.
Therefore, Singh stays at the clinic for the maximum duration on Monday
Ans: (Monday)
On a slow Thursday, only two patients are waiting at 9 a.m. After that two patients keep arriving at exact 15 minute intervals starting at 9:15 a.m. -- i.e. at 9:15 a.m., 9:30 a.m., 9:45 a.m. etc. Then the total duration in minutes when all three doctors are simultaneously free is
Video Explanation

Explanatory Answer

The above pattern continues.
Hence, there is no time where all the doctors are simultaneously free.
Ans: (0)
In a circle with centre O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is
Video Explanation

Explanatory Answer
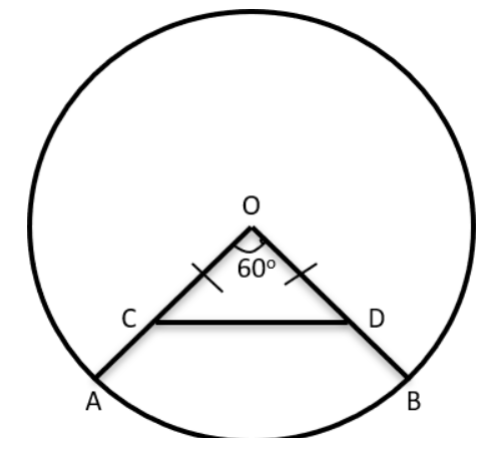
Given ∠AOB = 60°
Area of Sector AOB = 60/360 × π = π/6 ---(1)
Given OC = OD => ∠OCD = ∠ODC = 60°
△OCD is an Equilateral Triangle with side = a
Area(△OCD) = √3/4 × a × a ---(2)
Its given that Area(OCD) = 1/2 × Area(OAB)
a 2 (√3/4) = π / ( 6×2)
a = (π/ 3√3) 1/2
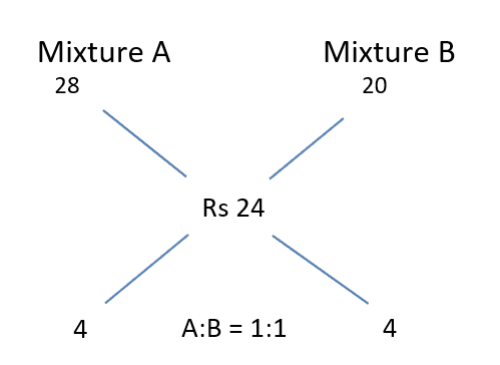
A trader sells 10 litres of a mixture of paints A and B, where the amount of B in the mixture does not exceed that of A. The cost of paint A per litre is Rs. 8 more than that of paint B. If the trader sells the entire mixture for Rs. 264 and makes a profit of 10%, then the highest possible cost of paint B, in Rs. per litre, is
Video Explanation

Explanatory Answer
Given, The amount of B in mixture ≤ Amount of A in mixture
Selling Price = Rs. 264 and Profit = 10 %
264 = 1.1 × CP
CP = 264/1.1 = Rs. 240 for 10 litres
CP per litre = Rs. 24
We also know that, CP per litre of A = CP per litre of B + 8 Let CP per litre of B = x So, CP per
litre of A = x + 8
Given Amount of B ≤ Amount of A,
Maximum possible cost of B occurs when B = A
We need to choose values for A and B in such a way that the quantities remain same.But A should
be 8 more than B
Therefore, A should have a CP per litre of Rs. 28 and B should have a CP per litre of Rs 20
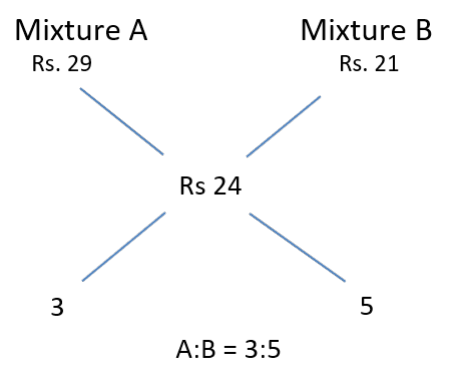
B cannot be assigned any more than this as the amount of B would become more than A
Example: Let us assign B to be Rs. 21 and A to be Rs. 29 which would result in a ratio of 3:5 where
B amounts more than A, which doesn’t satisfy the condition
Max possible cost of Paint B = Rs. 20 per litre
How many of the students surveyed supported proposal B, did not support proposal A and preferred Ragini as student union president?
Video Explanation

Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows
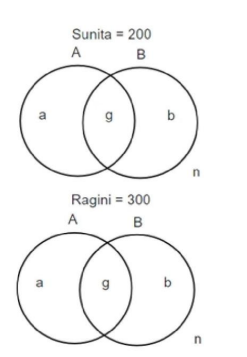
There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.
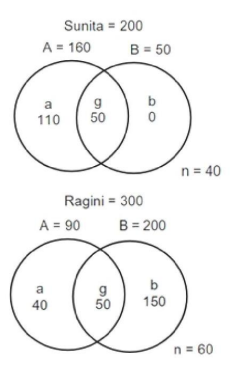
The students who supported proposal B but not A are b (Sunita) and b (Ragini). Among
them those supported Ragini are b (Ragini) 150. Ans: (150)
Students & Proposals
Students in a college are discussing two proposals --
A: a proposal by the authorities to introduce dress code on campus, and
B: a proposal by the students to allow multinational food franchises to set up outlets on college campus.
A student does not necessarily support either of the two proposals. In an upcoming election for student union president, there are two candidates in fray: Sunita and Ragini. Every student prefers one of the two candidates.
A survey was conducted among the students by picking a sample of 500 students. The following information was noted from this survey.
1) 250 students supported proposal A and 250 students supported proposal B.
2) Among the 200 students who preferred Sunita as student union president, 80% supported proposal A.
3) Among those who preferred Ragini, 30% supported proposal A.
4) 20% of those who supported proposal B preferred Sunita.
5) 40% of those who did not support proposal B preferred Ragini.
6) Every student who preferred Sunita and supported proposal B also supported proposal A.
7) Among those who preferred Ragini, 20% did not support any of the proposals.
Among the students surveyed who supported proposal A, what percentage preferred Sunita for student union president? [TITA]
Video Explanation

Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows

There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.

The required value is 160/250*100 = 64
What percentage of the students surveyed who did not support proposal A preferred Ragini as student union president? [TITA]
Video Explanation

Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows

There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.

The required answer is 210/250*100 = 84
What percentage of the students surveyed who supported both proposals A and B preferred Sunita as student union president?
Video Explanation

Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows

There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.

The required answer is 50/250*100 = 50
How many of the students surveyed supported proposal B, did not support proposal A and preferred Ragini as student union president?
Video Explanation

Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows

There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.

The students who supported proposal B but not A are b (Sunita) and b (Ragini). Among
them those supported Ragini are b (Ragini) 150. Ans: (150)
Among the students surveyed who supported proposal A, what percentage preferred Sunita for student union president? [TITA]
Video Explanation

Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows

There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.

The required value is 160/250*100 = 64
What percentage of the students surveyed who did not support proposal A preferred Ragini as student union president? [TITA]
Video Explanation

Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows

There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.

The required answer is 210/250*100 = 84
What percentage of the students surveyed who supported both proposals A and B preferred Sunita as student union president?
Video Explanation

Explanatory Answer
The set of students who like Sunita and Ragini are disjoint sets.
Hence, the Venn diagram can be drawn as follows

There are 500 students in all.
From statement (2)
Sunita = 200. Hence, Ragini = 300.
From statement (1) A (Sunita) + A (Ragini) = 250 and B (Sunita) + B (Ragini) = 250.
From (2), A (Sunita) = 160. Hence, A (Ragini) = 90.
From (4), B (Sunita) = 20 % of 250 = 50. Hence, B (Ragini) = 200.
From (6), g (Sunita) = 50 and hence, b (Sunita) = 0 and a (Sunita) = 110. Hence, n (Sunita) =
40.
From (7), n (Ragini) = 60
It is given that 250 support B, hence the other 250 do not support B.
From (5), (a + n) of Ragini = 40 % of 250 = 100. Hence, a (Ragini) = 40.
Thus, the final solution is as follows.

The required answer is 50/250*100 = 50
If a ‘Low Monsoon State’ is defined as a state with actual rainfall from June-August, 2019 of 750 mm or less, then what is the median ‘deviation from LPA’ (as defined in the Y-axis of the figure) of ‘Low Monsoon States’?
Video Explanation

Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.
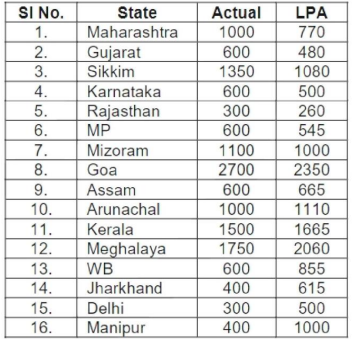
The Low monsoon states are Gujarat, Karnataka, Rajasthan, MP, Assam, WB, Jharkhand,
Delhi and Manipur. The deviation from LPA for these states are 25,20,15, 10,-10,-30,-35,-40
and -60. The median value is -10
What is the average rainfall of all states that have actual rainfall of 600 mm or less in 2019 and have a negative deviation from LPA?
Video Explanation

Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.

The states which have a negative deviation from LPA and have an actual rainfall of 600 mm
or less are Assam, WB, Jharkhand, Delhi and Manipur. The average rainfall in these states is
2300/5 = 460 mm
The LPA of a state for a year is defined as the average rainfall in the preceding 10 years considering the period of June-August. For example, LPA in 2018 is the average rainfall during 2009-2018 and LPA in 2019 is the average rainfall during 2010-2019. It is also observed that the actual rainfall in Gujarat in 2019 is 20% more than the rainfall in 2009. The LPA of Gujarat in 2019 is closest to
Video Explanation

Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.

The actual rainfall in Gujarat in 2019 is 600 mm. The rainfall in Gujarat in 2009 was 500 mm.
As the value of 500 is replaced by 600 in calculating the LPA, the LPA would increase by 10
as it is the average of 10 years.
Ans: (490 mm)
Rainfall
To compare the rainfall data, India Meteorological Department (IMD) calculated the Long Period Average (LPA) of rainfall during period June-August for each of the 16 states. The figure given below shows the actual rainfall (measured in mm) during June-August, 2019 and the percentage deviations from LPA of respective states in 2018. Each state along with its actual rainfall is presented in the figure.
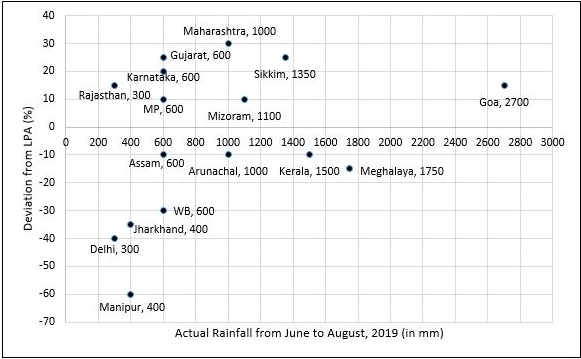
If a ‘Heavy Monsoon State’ is defined as a state with actual rainfall from June-August, 2019 of 900 mm or more, then approximately what percentage of ‘Heavy Monsoon States’ have a negative deviation from respective LPAs in 2019?
Video Explanation

Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.

The heavy monsoon states are Maharashtra, Sikkim, Mizoram, Goa, Arunachal, Kerala and
Meghalaya. Among these, Arunachal, Kerala and Meghalaya have a negative deviation from
respective LPAs in 2019. The required percentage = 3/7*100 = 42.86
If a ‘Low Monsoon State’ is defined as a state with actual rainfall from June-August, 2019 of 750 mm or less, then what is the median ‘deviation from LPA’ (as defined in the Y-axis of the figure) of ‘Low Monsoon States’?
Video Explanation

Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.

The Low monsoon states are Gujarat, Karnataka, Rajasthan, MP, Assam, WB, Jharkhand,
Delhi and Manipur. The deviation from LPA for these states are 25,20,15, 10,-10,-30,-35,-40
and -60. The median value is -10
What is the average rainfall of all states that have actual rainfall of 600 mm or less in 2019 and have a negative deviation from LPA?
Video Explanation

Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.

The states which have a negative deviation from LPA and have an actual rainfall of 600 mm
or less are Assam, WB, Jharkhand, Delhi and Manipur. The average rainfall in these states is
2300/5 = 460 mm
The LPA of a state for a year is defined as the average rainfall in the preceding 10 years considering the period of June-August. For example, LPA in 2018 is the average rainfall during 2009-2018 and LPA in 2019 is the average rainfall during 2010-2019. It is also observed that the actual rainfall in Gujarat in 2019 is 20% more than the rainfall in 2009. The LPA of Gujarat in 2019 is closest to
Video Explanation

Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.

The actual rainfall in Gujarat in 2019 is 600 mm. The rainfall in Gujarat in 2009 was 500 mm.
As the value of 500 is replaced by 600 in calculating the LPA, the LPA would increase by 10
as it is the average of 10 years.
Ans: (490 mm)
If a ‘Heavy Monsoon State’ is defined as a state with actual rainfall from June-August, 2019 of 900 mm or more, then approximately what percentage of ‘Heavy Monsoon States’ have a negative deviation from respective LPAs in 2019?
Video Explanation

Explanatory Answer
The actual rainfall in 2019 and the Long Period
Average (LPA) for the different states are as follows.

The heavy monsoon states are Maharashtra, Sikkim, Mizoram, Goa, Arunachal, Kerala and
Meghalaya. Among these, Arunachal, Kerala and Meghalaya have a negative deviation from
respective LPAs in 2019. The required percentage = 3/7*100 = 42.86
Apart from Chinese and English, which languages are spoken by Team 1?
Video Explanation

Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.
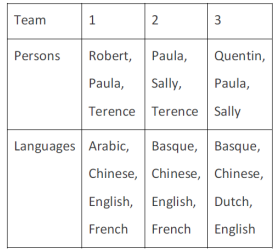
Languages spoken
In the table below the check marks indicate all languages spoken by five people: Paula, Quentin, Robert, Sally and Terence. For example, Paula speaks only Chinese and English.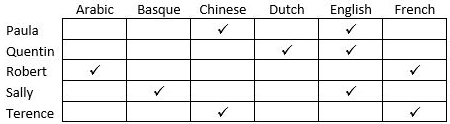
These five people form three teams, Team 1, Team 2 and Team 3. Each team has either 2 or 3 members. A team is said to speak a particular language if at least one of its members speak that language.
The following facts are known.
(1) Each team speaks exactly four languages and has the same number of members.
(2) English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team.
(3) None of the teams include both Quentin and Robert.
(4) Paula and Sally are together in exactly two teams.
(5) Robert is in Team 1 and Quentin is in Team 3.
Who among the following four is not a member of Team 2?
Video Explanation

Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.

Who among the following four people is a part of exactly two teams?
Video Explanation

Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.

Who among the five people is a member of all teams?
Video Explanation

Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.

Apart from Chinese and English, which languages are spoken by Team 1?
Video Explanation

Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.

Who among the following four is not a member of Team 2?
Video Explanation

Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.

Who among the following four people is a part of exactly two teams?
Video Explanation

Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.

Who among the five people is a member of all teams?
Video Explanation

Explanatory Answer
From (1) and (5), the persons in Team 1 speak English. Chinese. Arabic and French. (Robert
speaks both Arabic and French).
From (1) and (5), the persons in Team 3 speak. English, Chinese and Dutch. (Quentin speaks
Dutch and English). Since each person speaks two languages and each team speaks exactly
four languages, we need to find one person for Team 3. who speaks one language among
English, Chinese and Dutch and a different language apart from these three.
Since, Paula and Sally together speak Basque, Chinese and English and they are together in
exactly two teams, they cannot be in Team 1. They must be in Teams 2 and 3.
Hence, from (5) and the above, Paula, Quentin and Sally, (Basque. Chinese. Dutch and
English) are in Team 3. Since there are three persons in Team 3. Teams 1 and 2 should also
have three persons each. Team 1 speaks, English, Chinese, Arabic and French. Robert (Arabic
and French) is one of the team members. Now, two more persons, who speak languages
among the above four are to be selected. It is possible only with Paula and Terence.
From (2) Basque and French are spoken by two teams. Hence, Team 2 speaks these two
languages. Paula and Sally are there in Team 2 (Basque, Chinese and English). We need to
find one more person, who speaks one of these three languages and French. It is possible
with only Terence.

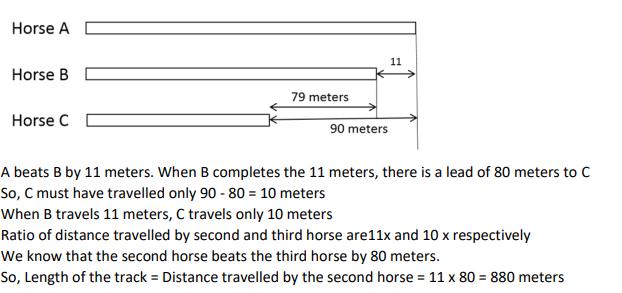
In a race of three horses, the first beat the second by 11 metres and the third by 90 metres. If the second beat the third by 80 metres, what was the length, in metres, of the racecourse?
Video Explanation

Explanatory Answer
The income of Amala is 20% more than that of Bimala and 20% less than that of Kamala. If Kamala's income goes down by 4% and Bimala's goes up by 10%, then the percentage by which Kamala's income would exceed Bimala's is nearest to
Video Explanation

Explanatory Answer
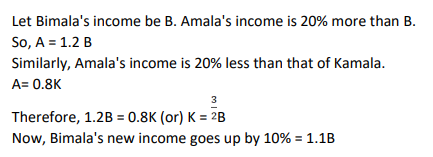

The number of the real roots of the equation 2cos(x(x + 1)) = 2x + 2-x is
Video Explanation

Explanatory Answer

If a1 + a2 + a3 + . + an = 3(2n+1 - 2), then a11 equals
Video Explanation

Explanatory Answer
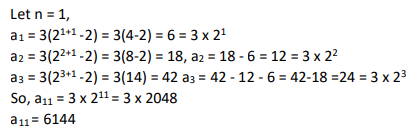
Two cars travel the same distance starting at 10:00 am and 11:00 am, respectively, on the same day. They reach their common destination at the same point of time. If the first car travelled for at least 6 hours, then the highest possible value of the percentage by which the speed of the second car could exceed that of the first car is
Video Explanation

Explanatory Answer

At their usual efficiency levels, A and B together finish a task in 12 days. If A had worked half as efficiently as she usually does, and B had worked thrice as efficiently as he usually does, the task would have been completed in 9 days. How many days would A take to finish the task if she works alone at her usual efficiency?
Video Explanation

Explanatory Answer

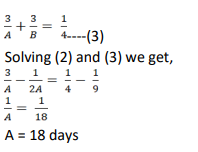
On selling a pen at 5% loss and a book at 15% gain, Karim gains Rs. 7. If he sells the pen at 5% gain and the book at 10% gain, he gains Rs. 13. What is the cost price of the book in Rupees?
Video Explanation

Explanatory Answer

The product of two positive numbers is 616. If the ratio of the difference of their cubes to the cube of their difference is 157 : 3, then the sum of the two numbers is
Video Explanation

Explanatory Answer
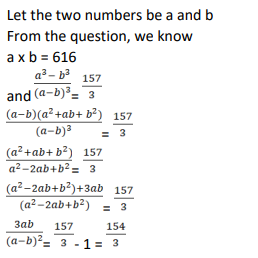

A person invested a total amount of Rs 15 lakh. A part of it was invested in a fixed deposit earning 6% annual interest, and the remaining amount was invested in two other deposits in the ratio 2 : 1, earning annual interest at the rates of 4% and 3%, respectively. If the total annual interest income is Rs 76000 then the amount (in Rs lakh) invested in the fixed deposit was
Video Explanation

Explanatory Answer

If the population of a town is p in the beginning of any year then it becomes 3+2p in the beginning of the next year. If the population in the beginning of 2019 is 1000, then the population in the beginning of 2034 will be
Video Explanation

Explanatory Answer

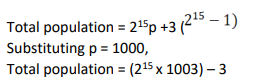
For any positive integer n, let f(n) = n(n + 1) if n is even, and f(n) = n + 3 if n is odd. If m is a positive integer such that 8f(m + 1) - f(m) = 2, then m equals
Video Explanation

Explanatory Answer
If n is even, f(n) = n (n + 1)
So, f (2) = 2(2+1) = 2 (3) = 6
If n is odd, f(n) = n + 3
f (1) = 1 + 3 = 4
It is given that, 8 x f(m+1) - f(m) =2
So, m can either be even or odd
Case-1: If m were even and m+1 odd
So, 8 x f(m+1) - f(m) =2
8(m + 4) - m (m + 1) = 2
8m + 32 - m2
- m = 2
m2
- 7m - 30 = 0
(m-10) (m+3) = 0
m = 10 or -3
m = 10, since m is positive
Case-2: If m were even and m+1 odd
8 x f(m+1) - f(m) =2
8 (m +1) (m + 2) - (m + 3) = 2
Now, let us substitute m = 1 which is the minimum possible value
8 (1 + 1) (1 + 2) - (1 + 3) 3
Case 2 does not work
Hence the answer is 10.
Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is
Video Explanation

Explanatory Answer
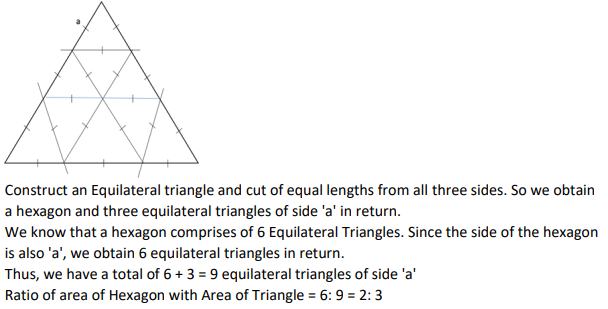
Meena scores 40% in an examination and after review, even though her score is increased by 50%, she fails by 35 marks. If her post-review score is increased by 20%, she will have 7 marks more than the passing score. The percentage score needed for passing the examination is
Video Explanation

Explanatory Answer
Meena scores 40 % in an exam
After review, she scores 50 % more => Increase of 50 % from 40 % = 40% + 20% = 60%
She fails by 35 marks, by scoring 60%
60% score = Pass mark - 35 ----- (1)
If her post review score is increased by 20%, she would have 7 more than the pass mark.
20% of 60% = 12 %
So, 60% + 12% = 72% of marks = Pass mark + 7 ------ (2)
So, 12% marks = 35 + 7 (5: 1 ratio)
So, similarly 12% can be re written as 10 % and 2 % (maintaining the 5:1 ratio)
Hence the pass percentage = 60 % + 10 % = 70%
(or)
Pass percentage = 72 % - 2 % = 70%
In a circle of radius 11 cm, CD is a diameter and AB is a chord of length 20.5 cm. If AB and CD intersect at a point E inside the circle and CE has length 7 cm, then the difference of the lengths of BE and AE, in cm, is
Video Explanation

Explanatory Answer

A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is
Video Explanation

Explanatory Answer

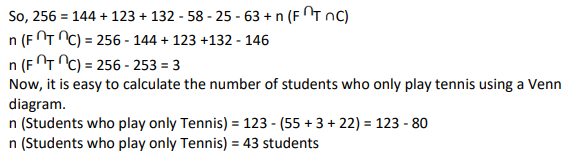
With rectangular axes of coordinates, the number of paths from (1,1) to (8,10) via (4,6), where each step from any point (x,y) is either to (x,y+1) or to (x+1,y) is
Video Explanation

Explanatory Answer

In a class, 60% of the students are girls and the rest are boys. There are 30 more girls than boys. If 68% of the students, including 30 boys,pass an examination, the percentage of the girls who do not pass is
Video Explanation

Explanatory Answer
Given that there are 60 % girls and 40 % boys
It is also given that there are 30 more girls than boys.
So, (60 % - 40 %) of total class strength = 30 students
=> 20 % of total class strength = 30 students
=> Total class strength = 30 x 5 = 150 students
It is also given that 68% of students pass the the examination, which includes 30 boys
So, Number of students passed = 68% of Total students
=> Number of students passed = x 150 = 102 students
=> Since the number of boys passed is 30,
=> Number of girls passed = 102 - 30 = 72
Total number of girls = x 150 = 90
Total number of girls = Girls who passed + Girls who did not pass
Girls who did not pass = 90 - 72 = 18
Percentage of girls who did not pass = 18/90 x 100 = 20 %
Which of the following CANNOT be determined uniquely based on the given information?
Video Explanation

Explanatory Answer
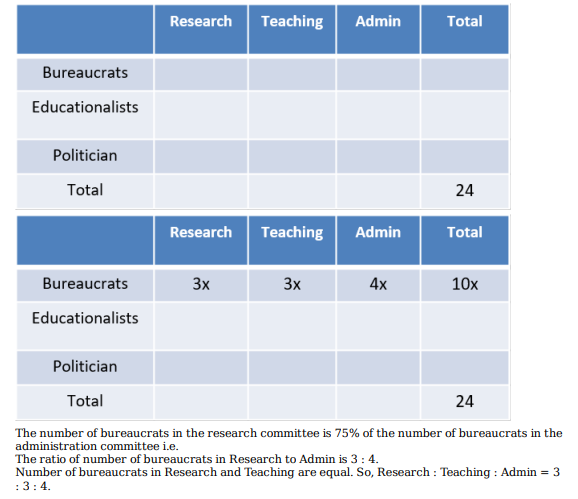
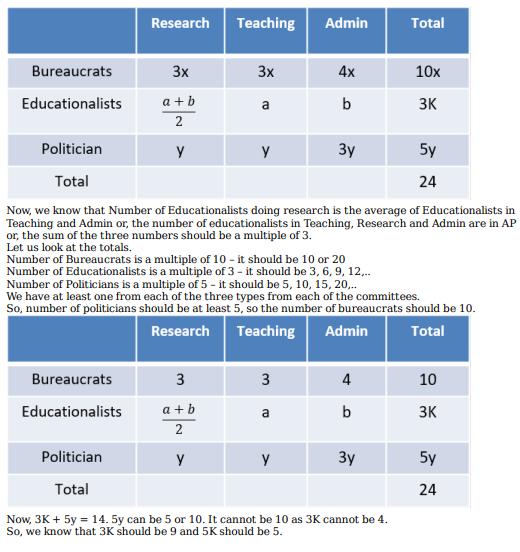
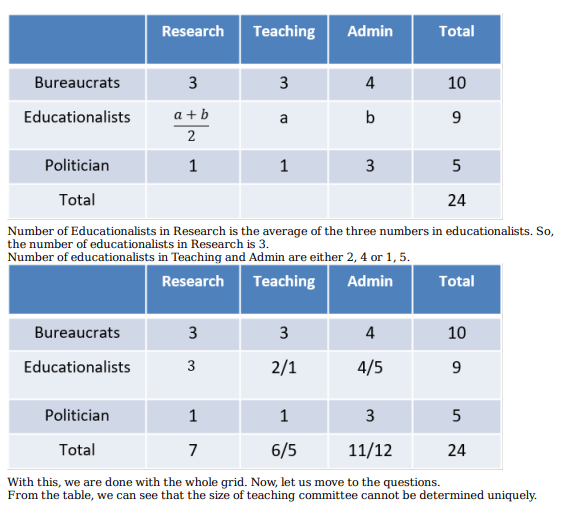
Twenty four people are part of three committees which are to look at research, teaching, and administration respectively. No two committees have any member in common. No two committees are of the same size. Each committee has three types of people: bureaucrats, educationalists, and politicians, with at least one from each of the three types in each committee. The following facts are also known about the committees:
1. The numbers of bureaucrats in the research and teaching committees are equal, while the number of bureaucrats in the research committee is 75% of the number of bureaucrats in the administration committee.
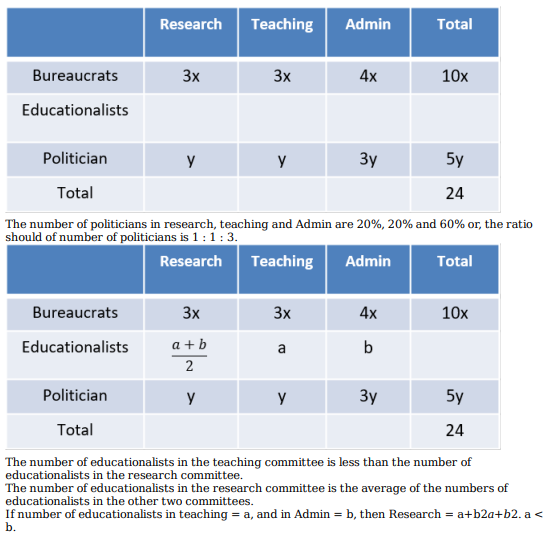
2. The number of educationalists in the teaching committee is less than the number of educationalists in the research committee. The number of educationalists in the research committee is the average of the numbers of educationalists in the other two committees.
3. 60% of the politicians are in the administration committee, and 20% are in the teaching committee.
Based on the given information, which of the following statements MUST be FALSE?
Video Explanation

Explanatory Answer



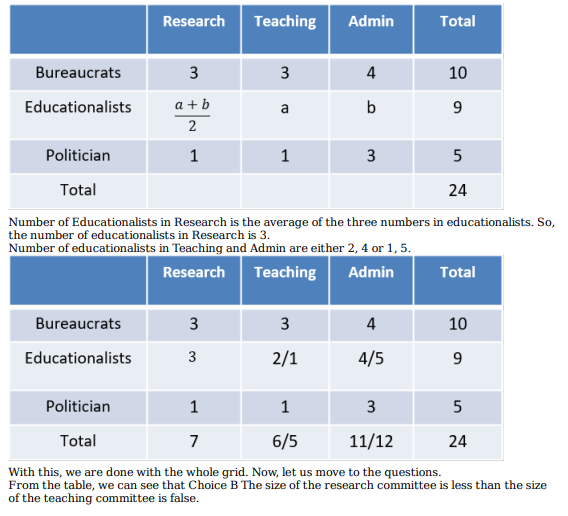
What is the number of bureaucrats in the administration committee? (TITA)
Video Explanation

Explanatory Answer



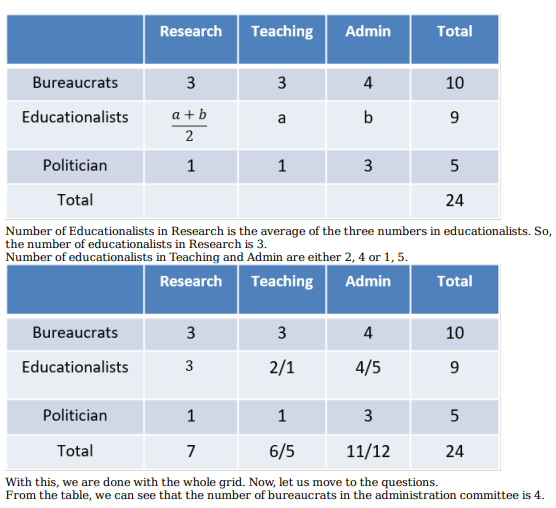
What is the number of educationalists in the research committee? (TITA)
Video Explanation

Explanatory Answer



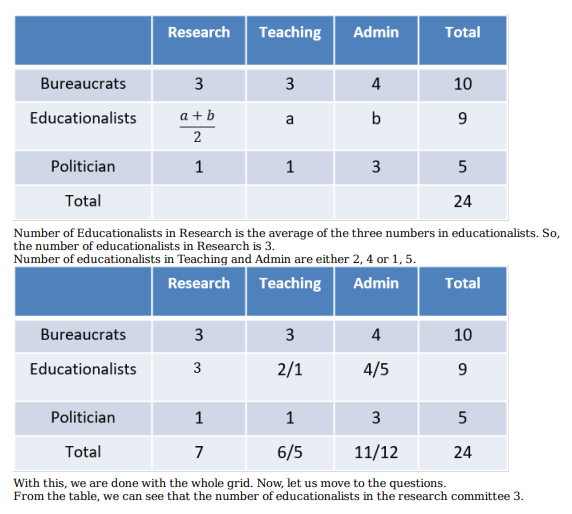
Which of the following CANNOT be determined uniquely based on the given information?
Video Explanation

Explanatory Answer




Based on the given information, which of the following statements MUST be FALSE?
Video Explanation

Explanatory Answer




What is the number of bureaucrats in the administration committee? (TITA)
Video Explanation

Explanatory Answer




What is the number of educationalists in the research committee? (TITA)
Video Explanation

Explanatory Answer