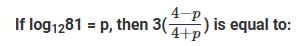Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
495
Learners
asked the doubt

Previous Year Questions
Let f(x)=min{2x2, 52 - 5x}, where x is any positive real number.Then the maximum possible value of f(x) is
Video Explanation

Explanatory Answer

If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
Video Explanation

Explanatory Answer
Given that out of 200 students, 105 like Pizza and 134 like Burger
In order to find the possible number of students who like only Burger, we need to find the range between the minimum and maximum possible number of students
Minimum possible number of Students who like only Burger:

For this, we must try to optimize the Venn diagram in such a way that it has maximum intersection
No of Students who like only Burger = 134 – 105= 29
Maximum possible number of Students who like only Burger:

For this, we must optimize the Venn diagram in such a way that it has minimum intersection
We know that total number of Students = 200
So, Minimum number of students who like both = 105 + 134 – 200 = 39 students
Students who like Burger = 134
Max. no of Students who like only Burger = 134 – 39 = 95
So range => 29 ≤ n ≤ 95
From the options, only (D) 93 lies within range
A tank is fitted with pipes, some filling it and the rest draining it. All filling pipes fill at the same rate, and all draining pipes drain at the same rate. The empty tank gets completely filled in 6 hours when 6 filling and 5 draining pipes are on, but this time becomes 60 hours when 5 filling and 6 draining pipes are on. In how many hours will the empty tank get completely filled when one draining and two filling pipes are on?
Video Explanation

Explanatory Answer
Given, Tank gets filled in 6 hours when 6 filling and 5 draining pipes are on
Let, F be the rate at which a single filling pipe fills the tanks and D be the rate at which a single
draining pipe drains the pipe
6F – 5D = 1616 th of the tank ---(1)
Also, Tank gets filled in 60 hours when 5 filling and 6 draining pipes are on
5F-6D = 160160 th of the tank ---(2)
Solving both (1) and (2) we get,
6F - 5D = 1/6
(-) 50 F - 60 D = 1/6
---------------------------
44F = 55D
F:D = 5:4
Replacing values in (1), 6F – 5D = 1/6
15D – 10D = 1/3
D = 1/15 and F = 1/12
When two filling pipes and one draining pipes are on,
2(1/6) – 1(/15) = (3/30) = 1/10 th of the tank
Therefore, they can fill the tank in 10 hours
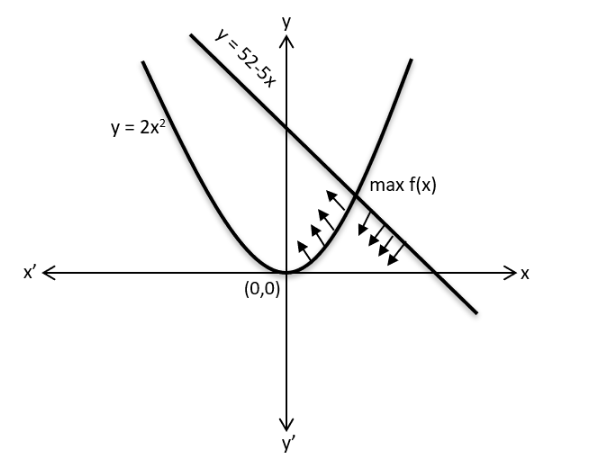
In a circle, two parallel chords on the same side of a diameter have lengths 4 cm and 6 cm. If the distance between these chords is 1 cm, then the radius of the circle, in cm, is
Video Explanation

Explanatory Answer
Given that Chords lie on the same side of diameter with lengths 4 cms and 6 cms
Draw a perpendicular from the origin to both the chords and mark the points of intersection as P
and Q respectively
Consider radius of circle as ‘r’ and distance OP as ‘x’
Draw lines from origin to the end of the chord and mark the points as D and B respectively
Thus, △OQB and △OPD form a right Triangle
Applying Pythagoras Theorem on both triangles,
(x+1) 2 +2 2 = r 2 ---(1)
x 2 +3 2 = r 2 ---(2)
We find that there is an increase and decrease by 1 in both equations
So, x 2 = 2 2 , x=2
r 2 = 2 2 +3 2 = 4+9 = 13
r = √13 cms
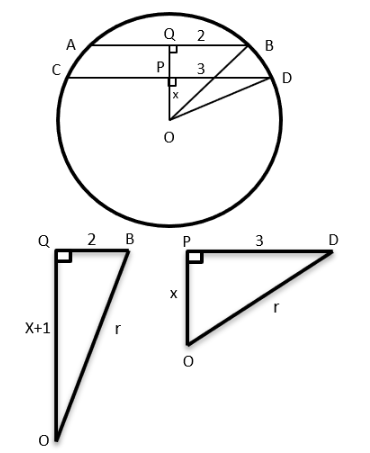
In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is
Video Explanation

Explanatory Answer
Given Area (ABCD) = 72 sq cm, CD = 9cms, AD = 16cms
Area of Parallelogram = Base × Height
CD × 16 = 72
CD = 72167216 cms
We extend CD till P such that ∠APD = 90°
So, again by applying the area formula considering CD as base
CD × AP = Area of Parallelogram ABCD
9 × AP = 72
AP = 8 cms
We have AP = 8 cms, AD = 16 cms We observe that the ratio of the sides form a 1 : √3 : 2 triangle Therefore DP = 8√3 cms Area (△APD) = 1/2 × AD × DP = 1/2 × 8 × 8√3 sq cms Area (△APD) = 32 √3 sq cms
Humans and robots can both perform a job but at different efficiencies. Fifteen humans and five robots working together take thirty days to finish the job, whereas five humans and fifteen robots working together take sixty days to finish it. How many days will fifteen humans working together (without any robot) take to finish it?
Video Explanation

Explanatory Answer
Let a Human complete ‘H’ units of work per day and a Robot complete ‘R’ units of work per day
Given,
15H + 5R = (1/30) th work per day --- (1)
5H + 15R = (1/60) th work per day --- (2)
Dividing (1) and (2) by 5 and solving,
3H + R = (1/150) and H + 3R = (1/300)
9H + 3R = 1/50
(-) H + 3R = 1/300
---------------------------
8H = 1/50 - 1/300 => 8H = 1/60
H = 1/480
Work done by 15 Humans in a day = 15/480 = 1/32
No of days required for 15 humans to complete the work = 32 days
If log2(5 + log3a) = 3 and log5(4a + 12 + log2b) = 3, then a + b is equal to
Video Explanation

Explanatory Answer
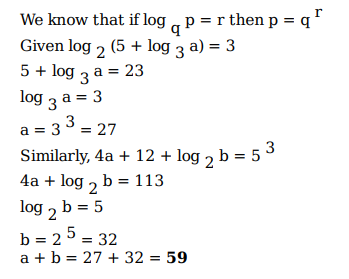
Raju and Lalitha originally had marbles in the ratio 4 : 9. Then Lalitha gave some of her marbles to Raju. As a result, the ratio of the number of marbles with Raju to that with Lalitha became 5 : 6. What fraction of her original number of marbles was given by Lalitha to Raju?
Video Explanation

Explanatory Answer

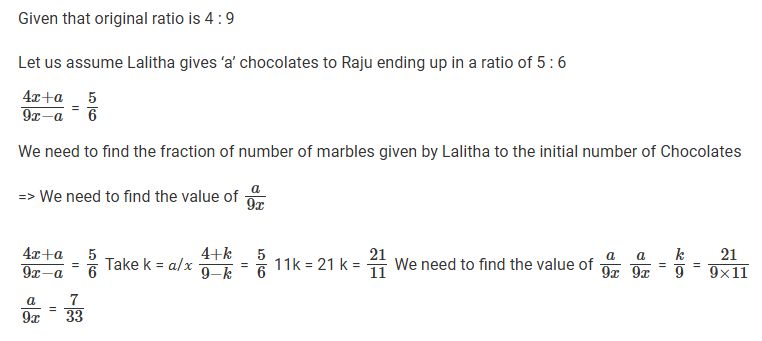
Given that x2018 y2017 = 1/2 and x2016 y2019 = 8, the value of x2 + y3 is
Video Explanation

Explanatory Answer
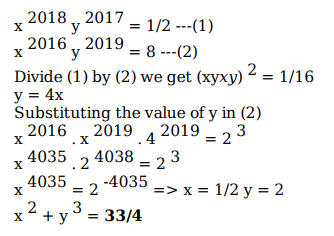
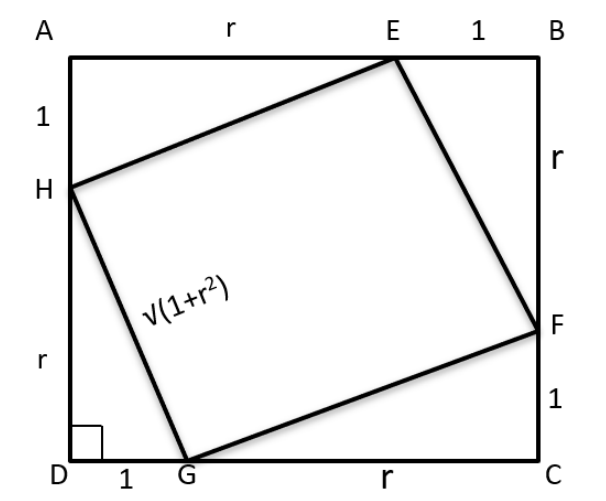
Points E, F, G, H lie on the sides AB, BC, CD, and DA, respectively, of a square ABCD. If EFGH is also a square whose area is 62.5% of that of ABCD and CG is longer than EB, then the ratio of length of EB to that of CG is:
Video Explanation

Explanatory Answer


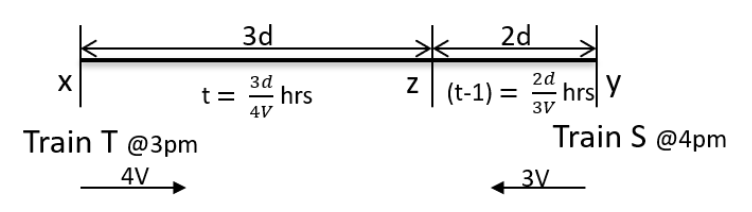
Train T leaves station X for station Y at 3 pm. Train S, traveling at three quarters of the speed of T, leaves Y for X at 4 pm. The two trains pass each other at a station Z, where the distance between X and Z is three-fifths of that between X and Y. How many hours does train T take for its journey from X to Y?
Video Explanation

Explanatory Answer

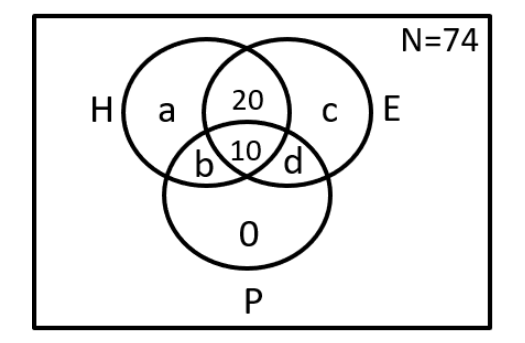
Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is
Video Explanation

Explanatory Answer
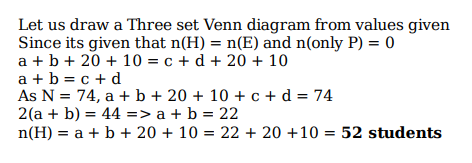
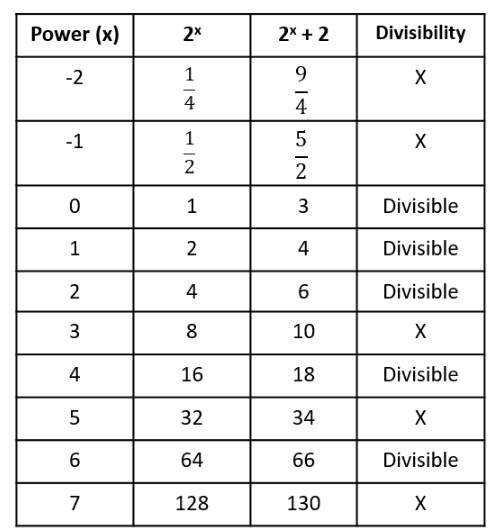
The number of integers x such that 0.25 < 2x < 200, and 2x + 2 is perfectly divisible by either 3 or 4, is
Video Explanation

Explanatory Answer
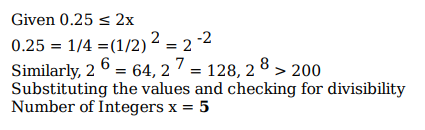
Let x, y, z be three positive real numbers in a geometric progression such that x < y < z. If 5x, 16y, and 12z are in an arithmetic progression then the common ratio of the geometric progression is
Video Explanation

Explanatory Answer

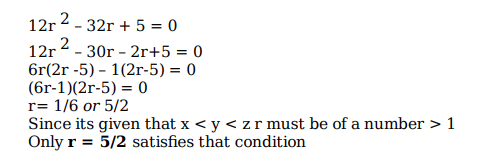
In an examination, the maximum possible score is N while the pass mark is 45% of N. A candidate obtains 36 marks, but falls short of the pass mark by 68%. Which one of the following is then correct?
Video Explanation

Explanatory Answer
Given Max. mark = N and Pass mark = 45% of N
A scores 36 marks and falls short of the pass mark by 68%
This means the pass mark must be reduced by (100 - 68)% = 32%
So, A scored 32% (45% N) = 36
N = 250 marks
The only option whose range falls within the obtained value is (B) 243 ≤ N ≤ 252
Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?
Video Explanation

Explanatory Answer
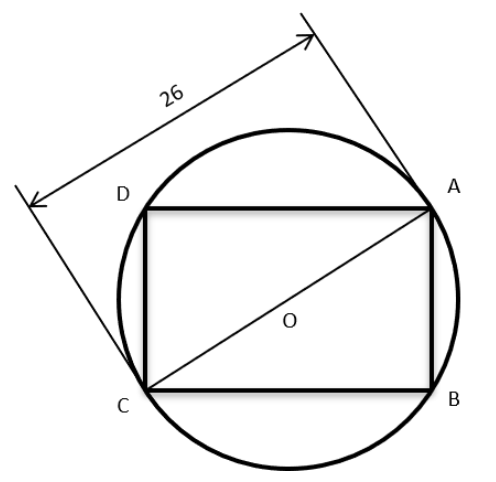
Since, ABCD is a rectangle inscribed inside a circle
ABC must be a Right triangle
Given that radius of Circle = 13 cms
5, 12, 13 forms a Pythagorean Triplet
10, 24, 26 is also a Pythagorean triplet
So, 10 and 24 are possible length and breadth of ABCD
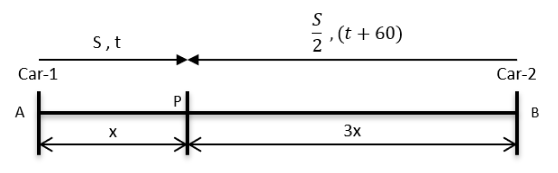
Point P lies between points A and B such that the length of BP is thrice that of AP. Car 1 starts from A and moves towards B. Simultaneously, car 2 starts from B and moves towards A. Car 2 reaches P one hour after car 1 reaches P. If the speed of car 2 is half that of car 1, then the time, in minutes, taken by car 1 in reaching P from A is:
Video Explanation

Explanatory Answer

If u2 + (u−2v−1)2 = −4v(u + v), then what is the value of u + 3v?
Video Explanation

Explanatory Answer
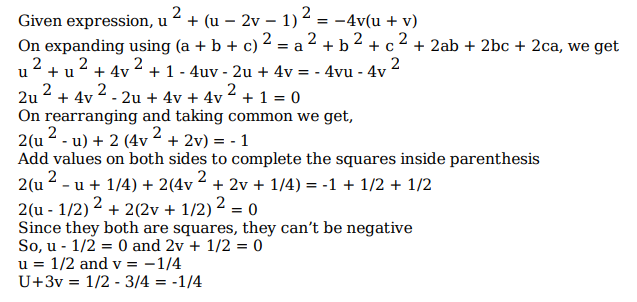
John borrowed Rs. 2,10,000 from a bank at an interest rate of 10% per annum, compounded annually. The loan was repaid in two equal instalments, the first after one year and the second after another year. The first instalment was interest of one year plus part of the principal amount, while the second was the rest of the principal amount plus due interest thereon. Then each instalment, in Rs., is:
Video Explanation

Explanatory Answer


How many numbers with two or more digits can be formed with the digits 1, 2, 3, 4, 5, 6, 7, 8, and 9 so that in every such number, each digit is used at most once and the digits appear in the ascending order?
Video Explanation

Explanatory Answer

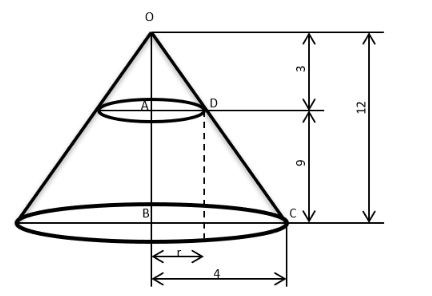
A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With π = 22/7, the volume, in cubic ft, of the remaining part of the cone is:
Video Explanation

Explanatory Answer

If x is a positive quantity such that 2x = 3log52 , then x is equal to
Video Explanation

Explanatory Answer

While multiplying three real numbers, Ashok took one of the numbers as 73 instead of 37. As a result, the product went up by 720. Then the minimum possible value of the sum of squares of the other two numbers is:
Video Explanation

Explanatory Answer
Let the three real numbers be a, b, c. c is taken as 73 instead of 37
So, 73ab = 37ab + 720
36 ab = 720
ab = 720/36 = 20
We know, AM ≥ GM
(a²+b²) / 2 ≥ ab
(a 2 + b 2 ) ≥ 2ab
(a 2 + b 2 ) ≥ 40
(Or)
ab = 20
(a,b) = (√20, √20)
(a 2 + b 2 ) = 20 + 20 = 40
Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,. will be
Video Explanation

Explanatory Answer
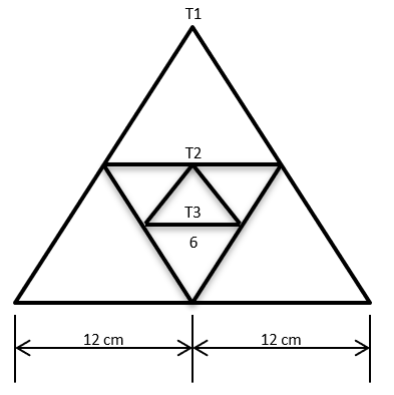
As the triangle progresses infinitely and the side length decreases, it follows an infinite GP series
As the sides decrease by half, their areas decrease by 1/4
We know, Area of an Equilateral Triangle = √3/4 × a 2
Area of T1 = √3/4 × 24 × 24 = 144 √3 sq cms
Sum of an Infinite GP = a / 1−r where a = 144 √3 , r = 1/4
Sum of areas ( T1, T2, T3,) = 144√3 / {1−(1/4)} = 4×144√3 / 3
Therefore, Sum of areas= 192 √3 sq cms.
When they work alone, B needs 25% more time to finish a job than A does. They two finish the job in 13 days in the following manner: A works alone till half the job is done, then A and B work together for four days, and finally B works alone to complete the remaining 5% of the job. In how many days can B alone finish the entire job?
Video Explanation

Explanatory Answer
Its given that B needs 25% more time than A
So, if Time taken by A = 4x days, Time taken by B = 5x days
A does half the work, So A works alone for 2x days --- (1)
A and B work for 4 days --- (2)
B works alone for 5x/20= x/4 days --- (3)
Total working days = 13
(1) + (2) + (3) = 13
2x + 4 + x/4 = 13 we get, x = 4
So, B alone can do the work in 5 × 4 = 20 days
Hence, the answer is 20 days
A wholesaler bought walnuts and peanuts, the price of walnut per kg being thrice that of peanut per kg. He then sold 8 kg of peanuts at a profit of 10% and 16 kg of walnuts at a profit of 20% to a shopkeeper. However, the shopkeeper lost 5 kg of walnuts and 3 kg of peanuts in transit. He then mixed the remaining nuts and sold the mixture at Rs. 166 per kg, thus making an overall profit of 25%. At what price, in Rs. per kg, did the wholesaler buy the walnuts?
Video Explanation

Explanatory Answer
Let the wholesaler bought walnuts and peanuts at Rs 3x and Rs x respectively
He sold 8kgs of Peanuts to the shopkeeper at 10% Profit
Cost price of the Peanuts bought by the shopkeeper = Rs. 1.1x per kg
Similarly, he sold 16 kgs of Walnuts to the shopkeeper at 20% Profit
Cost price of the Walnuts bought by the shopkeeper = 1.2 × 3x = Rs. 3.6x per Kg
He lost 5 kgs of Walnuts and 3 Kgs of Peanuts in transit
Remaining = 16 - 5 = 11 kgs of Walnuts & 8-3 = 5 kgs of Peanuts
He mixes them together and sells them at Rs. 166 per kg, making an overall Profit of 25%
Selling Price = 5/4 × Cost Price
Overall Cost Price = Rs.(3.6 × 16x + 1.1 × 8x)
Overall Selling Price = Rs. 16 × 166
Overall Selling Price = 5/4 × Overall Cost Price
(3.6 × 16x + 1.1 × 8x) × 5/4 = 16 × 166
( ( 57.6 × 8.8) x ) × 5/4 = 16 × 166
x = Rs. 32
Cost price per Kg of Walnuts bought by the Wholesaler = Rs. 3x = 3 × 32 = >Rs. 96
Two types of tea, A and B, are mixed and then sold at Rs. 40 per kg. The profit is 10% if A and B are mixed in the ratio 3 : 2, and 5% if this ratio is 2 : 3. The cost prices, per kg, of A and B are in the ratio
Video Explanation

Explanatory Answer
Let Tea A and B be sold at Rs.a and Rs.b respectively
When A and B are mixed in the ratio 3 : 2 and sold at a profit of 10% at Rs.40 per Kg
3a+2b / 5 = 40/1.1------(1)
When A and B are mixed in the ratio 2 : 3 and sold at a profit of 5% at Rs.40 per Kg
2a+3b/5 = 40/1.05 ------(2)
Solving equations (1) and (2), we get
1.1 × (3a+2b/5) = 1.05 × (2a+3b/5)
11/10 × (3a + 2b) = 21/20 × (2a + 3b)
66a + 44b = 42a + 63b
24a = 19b
a/b = 19/24
So, the cost prices per Kg of A and B are in the ratio 19 : 24
A CAT aspirant appears for a certain number of tests. His average score increases by 1 if the first 10 tests are not considered, and decreases by 1 if the last 10 tests are not considered. If his average scores for the first 10 and the last 10 tests are 20 and 30, respectively, then the total number of tests taken by him is
Video Explanation

Explanatory Answer
Let there be 'n' tests and the Overall Average score be k
Average (n) = k => Total marks = nk
So, when we ignore the first 10 questions,
Average (n-10) = k+1
Similarly, if we ignore the last 10 questions,
Average (first (n-10)) = k-1
It is given that when the first 10 tests are not considered, the overall average increases by 1
(Each question carries 20 marks)
Total marks – 20×10 = (k+1) (n-10)
kn – 200 = (k+1) (n-10) ---(1)
Similarly, If the last 10 tests are not considered, the overall average decreases by 1 (Each
question carries 30 marks)
kn - 300 = (k-1) (n-10) ---(2)
Solving (1) and (2), we get
kn - 200 = (k+1) (n-10)
(-) kn - 300 = (k-1) (n-10)
-------------------------------------
100 = 2(n-10)
50 = n-10
n = 60 questions
The distance from A to B is 60 km. Partha and Narayan start from A at the same time and move towards B. Partha takes four hours more than Narayan to reach B. Moreover, Partha reaches the mid-point of A and B two hours before Narayan reaches B. The speed of Partha, in km per hour, is
Video Explanation

Explanatory Answer
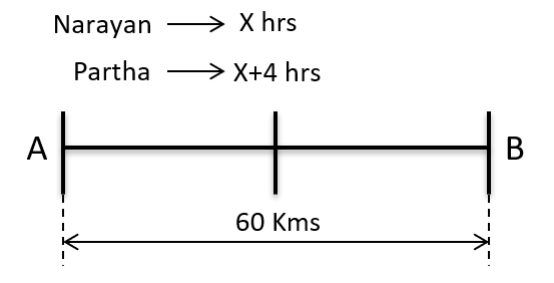
Let Narayanan take X hrs to reach B then Partha would take X + 4 hrs
Its given that Partha reaches the mid-point of A and B two hours before Narayan reaches B
X+4 / 2 = X – 2 => X=8 hrs
So, Partha would take 8+4 = 12 hrs to travel 60 Kms at a speed of 60/12 Kmph
Speed of Partha = 5 Kmph
If f(x + 2) = f(x) + f(x + 1) for all positive integers x, and f(11) = 91, f(15) = 617, then f(10) equals.
Video Explanation

Explanatory Answer
Given, f(x+2) = f(x) + f(x+1) f(11) = 91, f(15) = 617
We get 91 + f(12) = f(13)
Let f(12) be equal to some value ‘a’
So, 91 + a = f(13).
f(12) + f(13) = f(14)
a + 91 + a = f(14)
So, f(14) = 2a + 91 f(13) + f(14) = 617
So, 91 + a + 2a + 91 = 617
3a + 182 = 617
a = 145
Substituting the value of a and f(11), we get
f(10)+ 91 = 145
f(10) = 54
In a circle with centre O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is
Video Explanation

Explanatory Answer
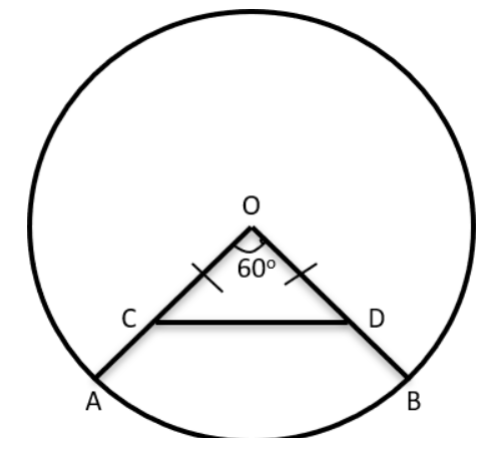
Given ∠AOB = 60°
Area of Sector AOB = 60/360 × π = π/6 ---(1)
Given OC = OD => ∠OCD = ∠ODC = 60°
△OCD is an Equilateral Triangle with side = a
Area(△OCD) = √3/4 × a × a ---(2)
Its given that Area(OCD) = 1/2 × Area(OAB)
a 2 (√3/4) = π / ( 6×2)
a = (π/ 3√3) 1/2
A trader sells 10 litres of a mixture of paints A and B, where the amount of B in the mixture does not exceed that of A. The cost of paint A per litre is Rs. 8 more than that of paint B. If the trader sells the entire mixture for Rs. 264 and makes a profit of 10%, then the highest possible cost of paint B, in Rs. per litre, is
Video Explanation

Explanatory Answer
Given, The amount of B in mixture ≤ Amount of A in mixture
Selling Price = Rs. 264 and Profit = 10 %
264 = 1.1 × CP
CP = 264/1.1 = Rs. 240 for 10 litres
CP per litre = Rs. 24
We also know that, CP per litre of A = CP per litre of B + 8 Let CP per litre of B = x So, CP per
litre of A = x + 8
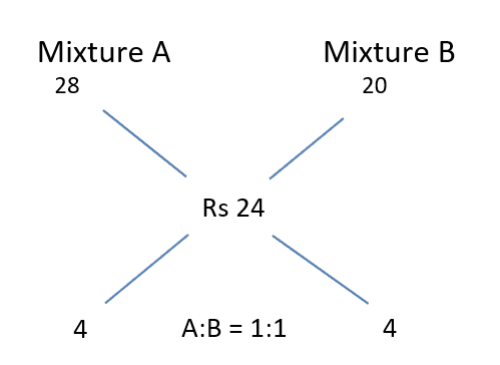
Given Amount of B ≤ Amount of A,
Maximum possible cost of B occurs when B = A
We need to choose values for A and B in such a way that the quantities remain same.But A should
be 8 more than B
Therefore, A should have a CP per litre of Rs. 28 and B should have a CP per litre of Rs 20
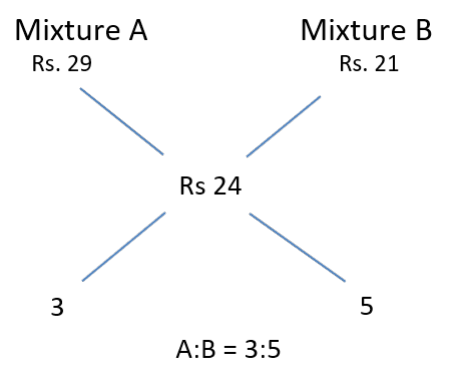
B cannot be assigned any more than this as the amount of B would become more than A
Example: Let us assign B to be Rs. 21 and A to be Rs. 29 which would result in a ratio of 3:5 where
B amounts more than A, which doesn’t satisfy the condition
Max possible cost of Paint B = Rs. 20 per litre
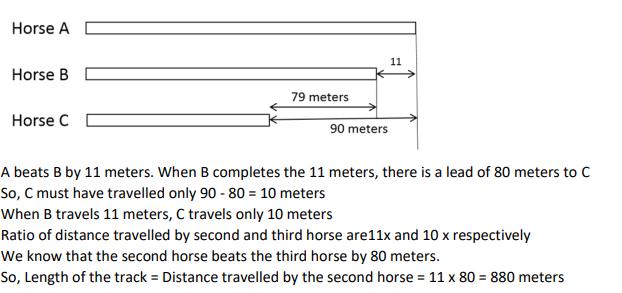
In a race of three horses, the first beat the second by 11 metres and the third by 90 metres. If the second beat the third by 80 metres, what was the length, in metres, of the racecourse?
Video Explanation

Explanatory Answer
The income of Amala is 20% more than that of Bimala and 20% less than that of Kamala. If Kamala's income goes down by 4% and Bimala's goes up by 10%, then the percentage by which Kamala's income would exceed Bimala's is nearest to
Video Explanation

Explanatory Answer
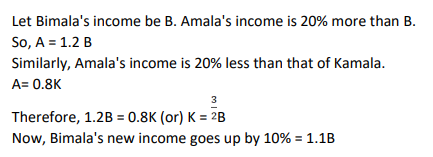

The number of the real roots of the equation 2cos(x(x + 1)) = 2x + 2-x is
Video Explanation

Explanatory Answer

If a1 + a2 + a3 + . + an = 3(2n+1 - 2), then a11 equals
Video Explanation

Explanatory Answer
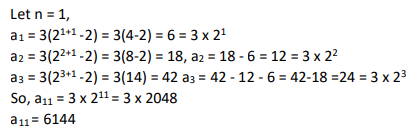
Two cars travel the same distance starting at 10:00 am and 11:00 am, respectively, on the same day. They reach their common destination at the same point of time. If the first car travelled for at least 6 hours, then the highest possible value of the percentage by which the speed of the second car could exceed that of the first car is
Video Explanation

Explanatory Answer

At their usual efficiency levels, A and B together finish a task in 12 days. If A had worked half as efficiently as she usually does, and B had worked thrice as efficiently as he usually does, the task would have been completed in 9 days. How many days would A take to finish the task if she works alone at her usual efficiency?
Video Explanation

Explanatory Answer

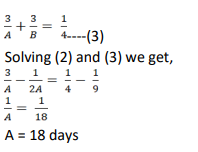
On selling a pen at 5% loss and a book at 15% gain, Karim gains Rs. 7. If he sells the pen at 5% gain and the book at 10% gain, he gains Rs. 13. What is the cost price of the book in Rupees?
Video Explanation

Explanatory Answer

The product of two positive numbers is 616. If the ratio of the difference of their cubes to the cube of their difference is 157 : 3, then the sum of the two numbers is
Video Explanation

Explanatory Answer
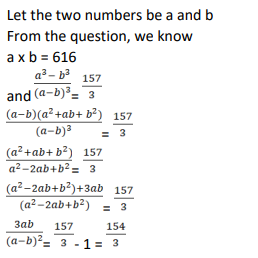

A person invested a total amount of Rs 15 lakh. A part of it was invested in a fixed deposit earning 6% annual interest, and the remaining amount was invested in two other deposits in the ratio 2 : 1, earning annual interest at the rates of 4% and 3%, respectively. If the total annual interest income is Rs 76000 then the amount (in Rs lakh) invested in the fixed deposit was
Video Explanation

Explanatory Answer

If the population of a town is p in the beginning of any year then it becomes 3+2p in the beginning of the next year. If the population in the beginning of 2019 is 1000, then the population in the beginning of 2034 will be
Video Explanation

Explanatory Answer

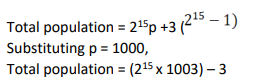
For any positive integer n, let f(n) = n(n + 1) if n is even, and f(n) = n + 3 if n is odd. If m is a positive integer such that 8f(m + 1) - f(m) = 2, then m equals
Video Explanation

Explanatory Answer
If n is even, f(n) = n (n + 1)
So, f (2) = 2(2+1) = 2 (3) = 6
If n is odd, f(n) = n + 3
f (1) = 1 + 3 = 4
It is given that, 8 x f(m+1) - f(m) =2
So, m can either be even or odd
Case-1: If m were even and m+1 odd
So, 8 x f(m+1) - f(m) =2
8(m + 4) - m (m + 1) = 2
8m + 32 - m2
- m = 2
m2
- 7m - 30 = 0
(m-10) (m+3) = 0
m = 10 or -3
m = 10, since m is positive
Case-2: If m were even and m+1 odd
8 x f(m+1) - f(m) =2
8 (m +1) (m + 2) - (m + 3) = 2
Now, let us substitute m = 1 which is the minimum possible value
8 (1 + 1) (1 + 2) - (1 + 3) 3
Case 2 does not work
Hence the answer is 10.
Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is
Video Explanation

Explanatory Answer
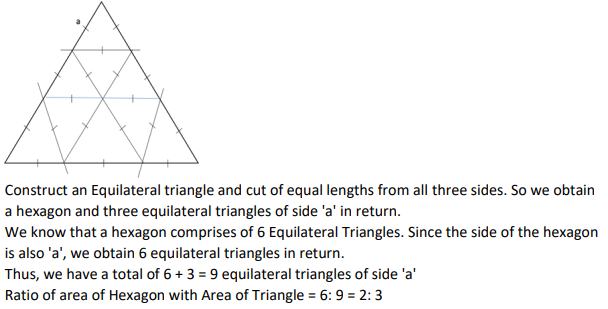
Meena scores 40% in an examination and after review, even though her score is increased by 50%, she fails by 35 marks. If her post-review score is increased by 20%, she will have 7 marks more than the passing score. The percentage score needed for passing the examination is
Video Explanation

Explanatory Answer
Meena scores 40 % in an exam
After review, she scores 50 % more => Increase of 50 % from 40 % = 40% + 20% = 60%
She fails by 35 marks, by scoring 60%
60% score = Pass mark - 35 ----- (1)
If her post review score is increased by 20%, she would have 7 more than the pass mark.
20% of 60% = 12 %
So, 60% + 12% = 72% of marks = Pass mark + 7 ------ (2)
So, 12% marks = 35 + 7 (5: 1 ratio)
So, similarly 12% can be re written as 10 % and 2 % (maintaining the 5:1 ratio)
Hence the pass percentage = 60 % + 10 % = 70%
(or)
Pass percentage = 72 % - 2 % = 70%
In a circle of radius 11 cm, CD is a diameter and AB is a chord of length 20.5 cm. If AB and CD intersect at a point E inside the circle and CE has length 7 cm, then the difference of the lengths of BE and AE, in cm, is
Video Explanation

Explanatory Answer

A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is
Video Explanation

Explanatory Answer

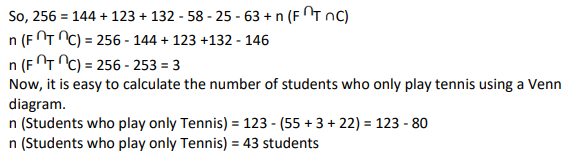
With rectangular axes of coordinates, the number of paths from (1,1) to (8,10) via (4,6), where each step from any point (x,y) is either to (x,y+1) or to (x+1,y) is
Video Explanation

Explanatory Answer