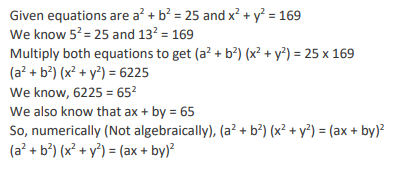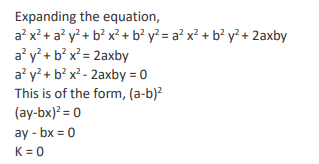Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
495
Learners
asked the doubt

Previous Year Questions
In a class, 60% of the students are girls and the rest are boys. There are 30 more girls than boys. If 68% of the students, including 30 boys,pass an examination, the percentage of the girls who do not pass is
Video Explanation

Explanatory Answer
Given that there are 60 % girls and 40 % boys
It is also given that there are 30 more girls than boys.
So, (60 % - 40 %) of total class strength = 30 students
=> 20 % of total class strength = 30 students
=> Total class strength = 30 x 5 = 150 students
It is also given that 68% of students pass the the examination, which includes 30 boys
So, Number of students passed = 68% of Total students
=> Number of students passed = x 150 = 102 students
=> Since the number of boys passed is 30,
=> Number of girls passed = 102 - 30 = 72
Total number of girls = x 150 = 90
Total number of girls = Girls who passed + Girls who did not pass
Girls who did not pass = 90 - 72 = 18
Percentage of girls who did not pass = 18/90 x 100 = 20 %
John gets Rs 57 per hour of regular work and Rs 114 per hour of overtime work. He works altogether 172 hours and his income from overtime hours is 15% of his income from regular hours. Then, for how many hours did he work overtime?
Video Explanation

Explanatory Answer
If John works the same number of regular and over-time hours say 'p'
The income would be 57p and 114p
Let's say that he works 'x' hours regularly and 'y' hours overtime.
So, the income would be 57x and 114y
we are told that 114y is 15% of 57x
114y = 0.15 * 57x
y = 0.075x
we also know that x+y = 172
therefore, x + 0.075x = 1.075x = 172
x = 160
y = 172 - 160 = 12
Therefore, the number of hours he worked Overtime is 12
A shopkeeper sells two tables, each procured at cost price p, to Amal and Asim at a profit of 20% and at a loss of 20%, respectively. Amal sells his table to Bimal at a profit of 30%, while Asim sells his table to Barun at a loss of 30%. If the amounts paid by Bimal and Barun are x and y, respectively, then (x - y) / p equals
Video Explanation

Explanatory Answer
The Shopkeeper procures the table at price 'p'
He gains 20% on the transaction with AmalSo, Amal buys the table at '1.2p'
Amal sells athe table at 30% profit,So the Selling Price of Amal = 1.3 * 1.2p = 1.56p
x = 1.56p
The Shopkeeper looses 20% on the transaction with Asim
So, Asim buys the table at '0.8p'
Asim sells athe table at 30% loss,
So the Selling Price of Asim = 0.7 * 0.8p = 0.56p
y = 0.56p
(x-y)/p = (1.56p - 0.56p)/p = 1.
Amal invests Rs 12000 at 8% interest, compounded annually, and Rs 10000 at 6% interest, compounded semi-annually, both investments being for one year. Bimal invests his money at 7.5% simple interest for one year. If Amal and Bimal get the same amount of interest, then the amount, in Rupees, invested by Bimal is
Video Explanation

Explanatory Answer

If 5x - 3y = 13438 and 5x-1 + 3y+1 = 9686 , then x+y equals
Video Explanation

Explanatory Answer

The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively. Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A. The strength, in percentage, of the resulting solution in vessel A is
Video Explanation

Explanatory Answer
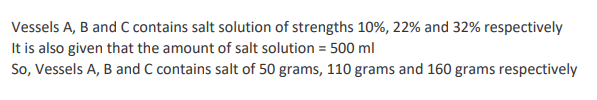

If (2n+1) + (2n+3) + (2n+5) + . + (2n+47) = 5280 , then what is the value of 1+2+3+ . +n ?
Video Explanation

Explanatory Answer

The number of common terms in the two sequences: 15, 19, 23, 27, , 415 and 14, 19, 24, 29, , 464 is
Video Explanation

Explanatory Answer
First series - 15, 19, 23, 27, , 415 -> Common difference = 4
Second series - 14, 19, 24, 29, , 464 -> Common difference = 5
Common terms in both sequences = 19, 39, 59, , (Common difference = LCM (4,5) = 20)
Now, observing the new series
19, 39, 59, , = (20 - 1), (40 -1), (60 -1), , (400-1) (There is no room for 419, as the first series ends
at 415)
399 = 400 - 1 = 20 x 20 -1
Hence, the number of common terms in the two sequences = 20
Mukesh purchased 10 bicycles in 2017, all at the same price. He sold six of these at a profit of 25% and the remaining four at a loss of 25%. If he made a total profit of Rs. 2000, then his purchase price of a bicycle, in Rupees, was
Video Explanation

Explanatory Answer
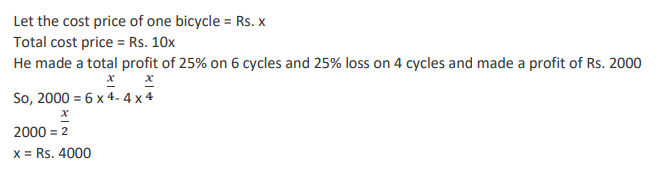
In a six-digit number, the sixth, that is, the rightmost, digit is the sum of the first three digits, the fifth digit is the sum of first two digits, the third digit is equal to the first digit, the second digit is twice the first digit and the fourth digit is the sum of fifth and sixth digits. Then, the largest possible value of the fourth digit is
Video Explanation

Explanatory Answer

The quadratic equation x2 + bx + c = 0 has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of b2 + c?
Video Explanation

Explanatory Answer

A man makes complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper to make a number of solid right circular cylinders of each type of metal. These cylinders have the same volume and each of these has radius 3 cm. If the total number of cylinders is to be kept at a minimum, then the total surface area of all these cylinders, in sq cm, is
Video Explanation

Explanatory Answer


The salaries of Ramesh, Ganesh and Rajesh were in the ratio 6:5:7 in 2010, and in the ratio 3:4:3 in 2015. If Ramesh's salary increased by 25% during 2010-2015, then the percentage increase in Rajesh's salary during this period is closest to
Video Explanation

Explanatory Answer
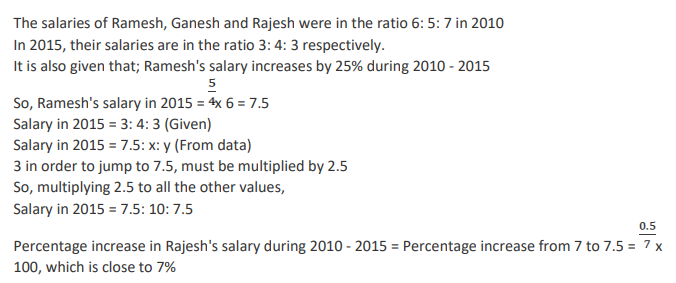
How many pairs (m,n) of positive integers satisfy the equation the equation m2 + 105 = n2?
Video Explanation

Explanatory Answer

Two ants A and B start from a point P on a circle at the same time, with A moving clock-wise and B moving anti-clockwise. They meet for the first time at 10:00 am when A has covered 60% of the track. If A returns to P at 10:12 am, then B returns to P at
Video Explanation

Explanatory Answer
We are told that, by the time A and B meet for the first time, A covers 60% of the distance, while B covers 40% of the distance.
So, the speeds of A and B are in the ratio 60:40 or 3:2
Hence, the time they take to cover a particular distance will be in the ratio 2:3
We know that A covers 60% of the distance at 10:00 AM and covers 100% of the distance at 10:12 AM.
That means A takes 12 minutes to cover 40% of the track. So to cover the entire track he must have
taken 12+12+6 = 30 minutes.
(because 40% + 40% + 20% = 100%)
Since the time taken by A and B to complete the track are in the ratio 2:3, the time taken by B to complete the track will be 45 minutes.
At 10:00 AM, B has covered 40% of the track. If we can find out what time does B take to complete the remaining 60% of the track, we can find the finish time of B.
Time required to complete 60% of the track = 60% of 45 = 27 minutes.
Hence, B complete one single round at 10:27 AM
Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is
Video Explanation

Explanatory Answer

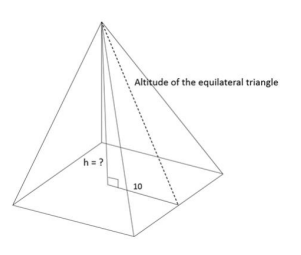
The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm. The vertical height of the pyramid, in cm, is
Video Explanation

Explanatory Answer

In an examination, the score of A was 10% less than that of B, the score of B was 25% more than that of C, and the score of C was 20% less than that of D. If A scored 72, then the score of D was
Video Explanation

Explanatory Answer

In an examination, Rama's score was one-twelfth of the sum of the scores of Mohan and Anjali. After a review, the score of each of them increased by 6. The revised scores of Anjali, Mohan, and Rama were in the ratio 11:10:3. Then Anjali's score exceeded Rama's score by
Video Explanation

Explanatory Answer


Anil alone can do a job in 20 days while Sunil alone can do it in 40 days. Anil starts the job, and after 3 days, Sunil joins him. Again, after a few more days, Bimal joins them and they together finish the job. If Bimal has done 10% of the job, then in how many days was the job done?
Video Explanation

Explanatory Answer

John jogs on track A at 6 kmph and Mary jogs on track B at 7.5 kmph. The total length of tracks A and B is 325 metres. While John makes 9 rounds of track A, Mary makes 5 rounds of track B. In how many seconds will Mary make one round of track A?
Video Explanation

Explanatory Answer
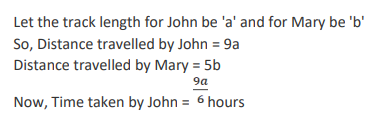

A cyclist leaves A at 10 am and reaches B at 11 am. Starting from 10:01 am, every minute a motorcycle leaves A and moves towards B. Forty-five such motorcycles reach B by 11 am. All motorcycles have the same speed. If the cyclist had doubled his speed, how many motorcycles would have reached B by the time the cyclist reached B?
Video Explanation

Explanatory Answer
It is given that the cyclist starts at 10:00 am from A and reaches B at 11:00 am
Now, Motorcyclists start every minute from 10:01 am, and 45 such motorcyclists reach B before
11:00 am
If they leave one by one every minute, the 45th motorcyclist would have left by 10:45 am to reach B
at 11:00 am.
Thus, time taken by one motorcyclist to reach B from A = 15 minutes.
Now, the cyclist doubles his speed. This means, he reaches B at 10:30 am
So, the last motorcyclist should have left A by 10:15 am
Thus, 15 motorcyclists would have reached B by the time the cyclist reaches B
Let A and B be two regular polygons having a and b sides, respectively. If b = 2a and each interior angle of B is 3/2 times each interior angle of A, then each interior angle, in degrees, of a regular polygon with a + b sides is
Video Explanation

Explanatory Answer
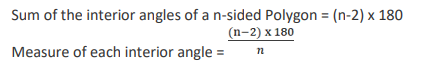

In 2010, a library contained a total of 11500 books in two categories - fiction and non-fiction. In 2015, the library contained a total of 12760 books in these two categories. During this period, there was 10% increase in the fiction category while there was 12% increase in the non-fiction category. How many fiction books were in the library in 2015?
Video Explanation

Explanatory Answer

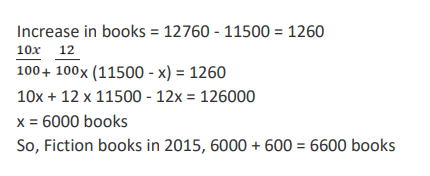
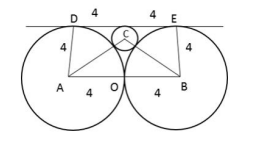
Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent, then the radius of the third circle, in cm, is
Video Explanation

Explanatory Answer

In a triangle ABC, medians AD and BE are perpendicular to each other, and have lengths
12 cm and 9 cm, respectively. Then, the area of triangle ABC, in sq cm, is
Video Explanation

Explanatory Answer
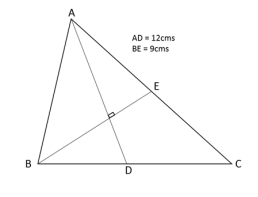

The average of 30 integers is 5. Among these 30 integers, there are exactly 20 which do not exceed 5. What is the highest possible value of the average of these 20 integers?
Video Explanation

Explanatory Answer
We are told that exactly 20 of the 30 integers do not exceed 5.
That means exactly 10 of the 30 integers do exceed 5.
In order to keep the average of the 20 integers as high as possible, we need to keep the average of
the 10 integers above 5 as low as possible. Since we are dealing with integers, the least value that
the 10 integers above 5 can take is 6.
So, the sum of the 10 integers = 10 * 6 = 60
So the sum of the remainng 20 integers = Total sum - 60 = 5 * 50 - 60 = 90
Hence the average of the remaining 20 is 90/20 = 4.5
How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3?
Video Explanation

Explanatory Answer
3 cases:
• 7 is in first place: 3 can go to 3 places, remaining 2 places will have 8 & 7 possibilities each
Hence, possible numbers are 3*8*7 = 168
• 7 is in second place: 3 can go to 2 places, first place will have 7 possibilities (excluding 0), and
remaining place will also have 7 possibilities
Hence, possible numbers are 2*7*7 = 98
• 7 is in third place: 3 can only go to one place, remaining 2 places have 7 possibilities each
Hence, possible numbers are 1*7*7 = 49
Therefore, total number of possibilities are 168 + 98 + 49 = 315
A sum of money is split among Amal, Sunil and Mita so that the ratio of the shares of Amal and Sunil is 3:2, while the ratio of the shares of Sunil and Mita is 4:5. If the difference between the largest and the smallest of these three shares is Rs 400, then Sunil’s share, in rupees, is
Video Explanation

Explanatory Answer

Aron bought some pencils and sharpeners. Spending the same amount of money as Aron, Aditya bought twice as many pencils and 10 less sharpeners. If the cost of one sharpener is 2 more than the cost of a pencil, then the minimum possible number of pencils bought by Aron and Aditya together is
Video Explanation

Explanatory Answer
Let cost of pencil be ‘x’ and sharpener be ‘x+2’.
Amount spent by Aron = p*x + s*(x+2)
Amount spent by Aditya = 2p*x + (s- 10)( x+2)
Therefore: px + sx + 2s = 2px + sx - 10x + 2s – 20
px - 10x - 20 = 0
x(p-10) = 20
Since p-10 > 0, p(min) = 11
Total pencils = p + 2p = 33
In May, John bought the same amount of rice and the same amount of wheat as he had bought in April, but spent 150 more due to price increase of rice and wheat by 20% and 12%, respectively. If John had spent 450 on rice in April, then how much did he spend on wheat in May?
Video Explanation

Explanatory Answer
In April, John bought ‘r’ amount of rice at ‘x’ price, and ‘w’ amount of wheat at ‘y’ price.
Money spent = r * x + w * y
Also, r*x = 450
In May, amount spent = r( 1.2x) + w(1.12y)
= 1.2r*x + 1.12w*y = (r*x + w*y) + 150
0.2r*x + 0.12w*y = 150
0.12w*y = 150 – 0.2*450 = 60
w*y = 60/0.12 = 500
Amount spent on wheat in May = 1.12*500 = 560
John takes twice as much time as Jack to finish a job. Jack and Jim together take one-thirds of the time to finish the job than John takes working alone. Moreover, in order to finish the job, John takes three days more than that taken by three of them working together. In how many days will Jim finish the job working alone?
Video Explanation

Explanatory Answer
Let’s assume the amount of work done by each person in a day:
John – x
Jack – 2x
If Jack and Jim together take 1/3 of the time that John takes, it means they together complete 3 times the work that John alone completes in a day.
Hence, Jack + Jim = 3x
Jim – x
Assuming the work to be done is 100 units.
Number of days taken by each person is:
John – 100/x
Jack – 50/x
Jim – 100/x
All 3 together – 25/x
Therefore, 100/x = 25/x + 3
100 = 25 + 3x
3x = 75
x = 25
Jim will finish the job alone in 100/x = 100/25 = 4 days
Let C1 and C2 be concentric circles such that the diameter of C1 is 2cm longer than that of C2. If a chord of C1 has length 6 cm and is a tangent to C2, then the diameter, in cm of C1 is
Video Explanation

Explanatory Answer
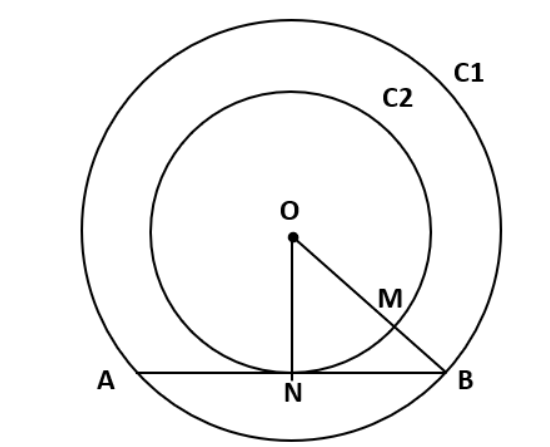
In the figure, ‘O’ is the centre of circles ‘C1’ and ‘C2’ with radii ‘ x ’ & ‘ y ’ respectively
If d1 – d2 = 2cm, x - y = 1cm
Hence, MB = 1cm
AB is a chord with 6cm length and tangent to C2.
Therefore, AN = NB = 3cm ; ON = y; OB = y + 1
In right triangle ONB:
(ON) 2 + (NB) 2 = (OB) 2
y 2 + 9 = (y+1) 2
9 = 2y + 1
2y + 8
y = 4
Therefore, x = y + 1 = 5cm
Diameter = 2x = 10cm
A and B are two points on a straight line. Ram runs from A to B while Rahim runs from B to A. After crossing each other, Ram and Rahim reach their destinations in one minutes and four minutes, respectively. If they start at the same time, then the ratio of Ram's speed to Rahim's speed is
Video Explanation

Explanatory Answer
![]()
Assuming Ram’s speed = ‘a’ and Rahim’s speed = ‘b’.
If they cross each other at time ‘t’:
Distance travelled by Ram = a*t
Distance travelled by Rahim = b*t
Further time taken by Ram to reach B = (Dist. Remaining/Speed) = (b*t)/a = 1min -------①
Similarly, further time taken by Rahim to reach A = (a*t)/b = 4min -------②
Assume ratio (a/b) = x
Therefore, ① becomes: t/x = 1 &
② becomes: t*x = 4
Multiplying both equations, we get: t 2 = 4
Therefore t = 2
Applying value of t, we get x = 2 = a/b
Two circular tracks T1 and T2 of radii 100 m and 20 m, respectively touch at a point A. Starting from A at the same time, Ram and Rahim are walking on track T1 and track T2 at speeds 15 km/hr and 5 km/hr respectively. The number of full rounds that Ram will make before he meets Rahim again for the first time is
Video Explanation

Explanatory Answer
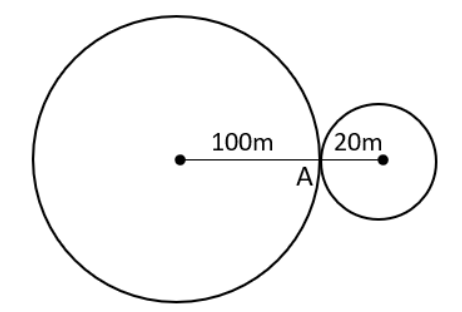
Circumference of T1 = 2π*100 = 200π
Time taken by Ram to reach A again = 200π/15 = 40π/3
Circumference of T2 = 2π*20 = 40π
Time taken by Rahim to reach A again = 40π/5
Ratio of the time taken by Ram & Rahim = (40π/3) /( 40 π/5) = 5/3
Ratio of time is inverse of ratio of distance travelled
Therefore, ratio of rounds travelled by Ram : Rahim = 3:5
Ram makes 3 rounds before he meets Rahim again
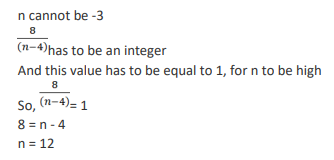
In how many ways can a pair of integers (x , a) be chosen such that x2 − 2 | x | + | a - 2 | = 0 ?
Video Explanation

Explanatory Answer
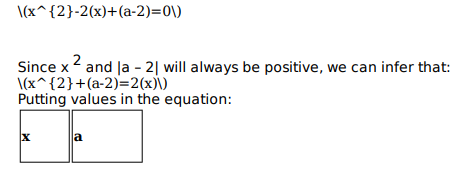
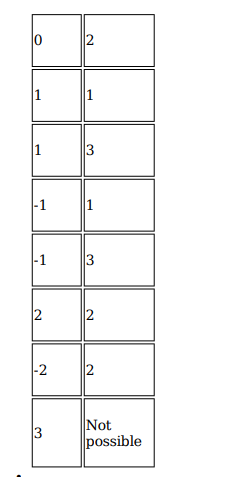
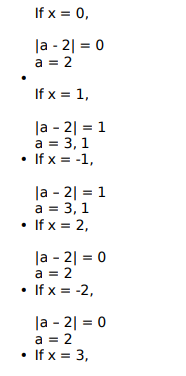

![]()
Video Explanation

Explanatory Answer
\((x^{2}-5x+7)^{(x+1)}=1\)
2 cases:
• Power is 0
x + 1 = 0
x = -1
• \(x^{2}-5x+7=1\)
\(x^{2}-5x+6=0\)
\(x^{2}-2x-3x+6=0\)
\(x(x-2)-3(x-2)=0\)
\((x-2)(x-3)=0\)
\(x=2, x=3\)
• \(x^{2}-5x+7=-1\) ; Given power is even
\(x^{2}-5x+8=0\)
No real roots
Hence, 3 integers (-1, 2, 3) satisfy the given equation
The sum of perimeters of an equilateral triangle and a rectangle is 90 cm. The area, T, of the triangle and the area , R, of the rectangle, both in sq cm, satisfy the relationship R = T2. If the sides of the rectangle are in the ratio 1 : 3, then the length, in cm, of the longer side of the rectangle, is
Video Explanation

Explanatory Answer
Let side of triangle be ‘a’; Breadth of rectangle = x; Length of rectangle = 3x
Therefore: 3a + 2(x+3x) = 90
3a + 8x = 90 ----------( i )
Also, R = T 2
x *3x = ( Ö 3a 2 /4) 2
3x 2 = 3a 4 /16
x = a 2 /4
Hence ( i ) becomes:
3a + 8(a 2 /4) = 90
3a + 2a 2 = 90
2a 2 + 3a -90 = 0
Solving the quadratic equation, we get a = 6
x = 9 ; 3x = 27
Hence, longer side = 27
The distance from B to C is thrice that from A to B. Two trains travel from A to C via B. The speed of train 2 is double that of train 1 while traveling from A to B and their speeds are interchanged while traveling from B to C. The ratio of the time taken by train 1 to that taken by train 2 in travelling from A to C is
Video Explanation

Explanatory Answer
BC = 3*AB
AB = x, BC = 3x
Let 2 trains be T1 & T2.
From A to B: Speed of T1 = s; Speed of T2 = 2s
From B to C: Speed of T1 = 2s; Speed of T2 = s
Total time taken by T1 (t1) = (x/ s)+( 3x/2s) = 5x/2s
Total time taken by T2 (t2) = (x/2s) + 3x/s) = 7x/2s
Ratio t1:t2 = 5x/2s:7x/2s = 5:7
Let f(x) = x2 + ax + b and g(x) = f(x + 1) - f(x - 1). If f(x) ≥ 0 for all real x, and g(20) = 72, then the smallest possible value of b is
Video Explanation

Explanatory Answer
g( 20) = f(21) – f(19)
72 = 21 2 + 21a + b – (19 2 + 19a + b)
72 = 40*2 + 2a
2a = -8
a = -4
f(x) = x 2 - 4x + b
Now, f(x) ≥ 0 for all real x
Therefore, D ≤ 0
16 – 4b ≤ 0
16 ≤ 4b
4 ≤ b
Hence, smallest possible value of b is 4
Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is
Video Explanation

Explanatory Answer
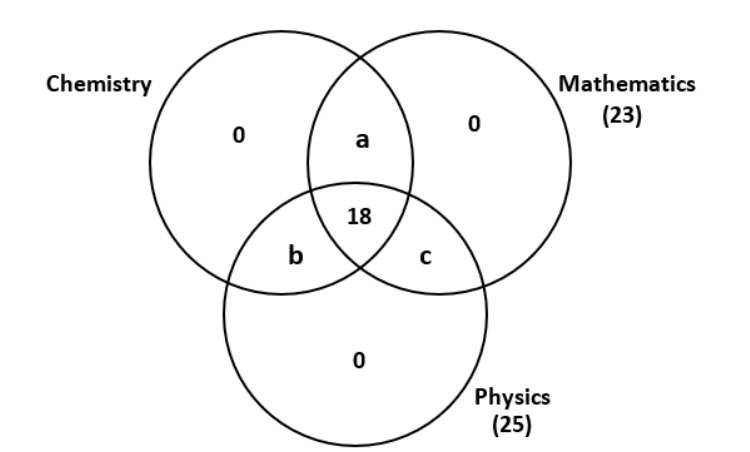
We can summarize the information given in the question as per the above Venn diagram.
We can conclude that:
a + c = 5
b + c = 7
Hence, b – a = 2
We have to minimize a + b.
Assuming if a = 0
Then b = 2 & c = 5
Therefore, number of students choosing Chemistry as one subject = 18 + 2 = 20