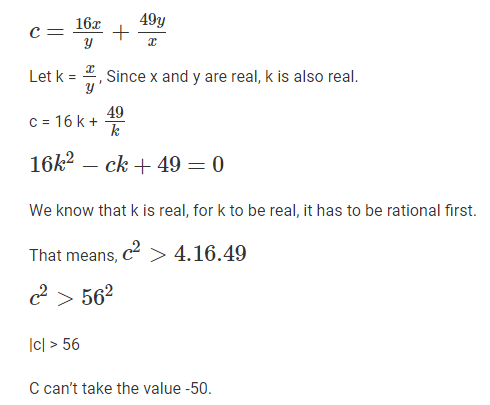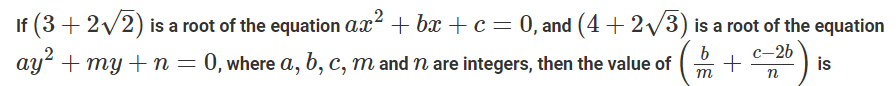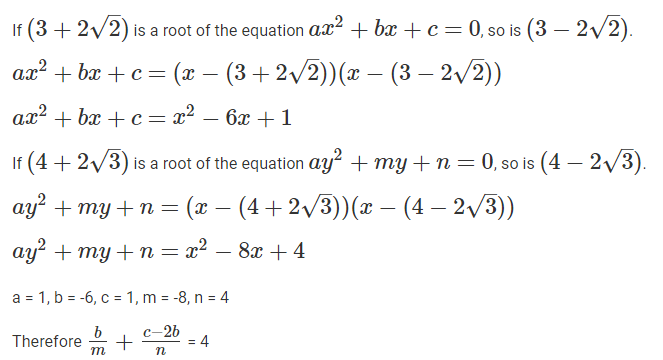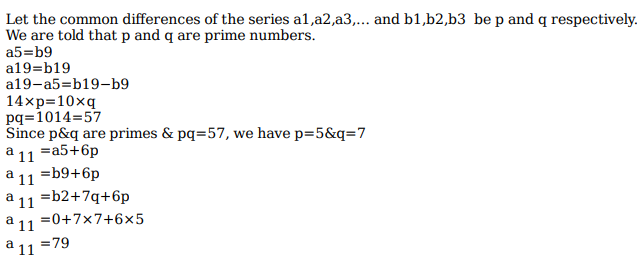Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
495
Learners
asked the doubt

Previous Year Questions
The number of ways of distributing 20 identical balloons among 4 children such that each child gets some balloons but no child gets an odd number of balloons, is
Video Explanation

Explanatory Answer
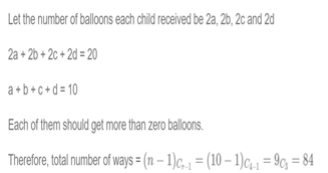
Let ABCD be a parallelogram such that the coordinates of its three vertices A, B, C are (1, 1), (3, 4) and (−2, 8), respectively. Then, the coordinates of the vertex D are
Video Explanation

Explanatory Answer

The lengths of all four sides of a quadrilateral are integer valued. If three of its sides are of length 1 cm, 2 cm and 4 cm, then the total number of possible lengths of the fourth side is
Video Explanation

Explanatory Answer
In any polygon, the largest side length should be less than the sum of the lengths of the other sides.
Let the fourth side be ‘x’.
Case i) x is the largest side.
x < 1 + 2 + 6
x < 7
x can take the following values, 4, 5, 6
Case ii)
4 is the largest side and x is less than 4.
4 < x + 1 +2
x > 1
x can take the values 2 or 3
So, x can take the values 2, 3, 4, 5, 6.
x can take 5 values.
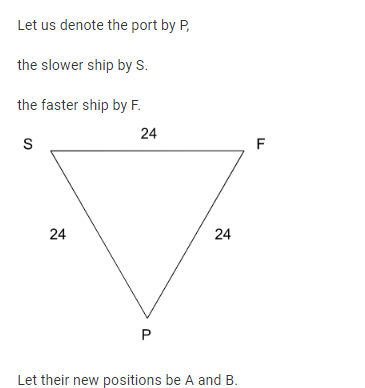
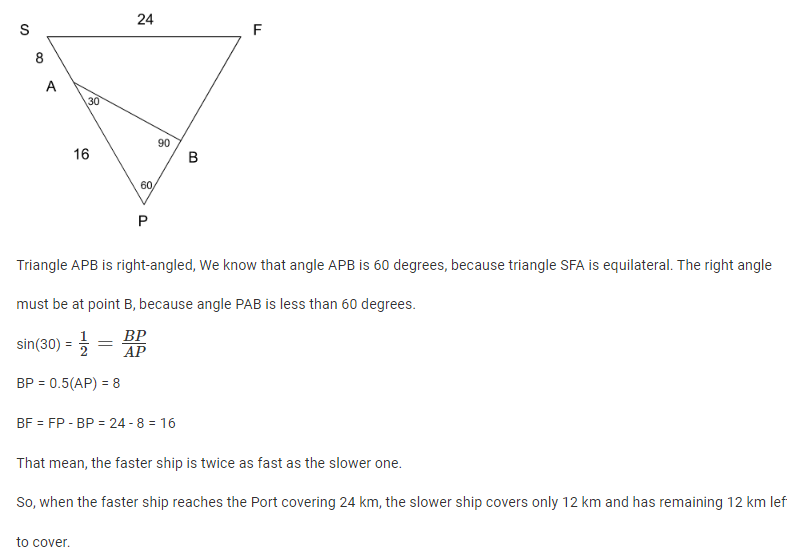
Two ships are approaching a port along straight routes at constant speeds. Initially, the two ships and the port formed an equilateral triangle with sides of length 24 km. When the slower ship travelled 8 km, the triangle formed by the new positions of the two ships and the port became right-angled. When the faster ship reaches the port, the distance, in km, between the other ship and the port will be
Video Explanation

Explanatory Answer
A donation box can receive only cheques of ₹100, ₹250, and ₹500. On one good day, the donation box was found to contain exactly 100 cheques amounting to a total sum of ₹15250. Then, the maximum possible number of cheques of ₹500 that the donation box may have contained, is
Video Explanation

Explanatory Answer
Since the total donation amount is 15,250 rupees, there should be at least one 250 rupee note. The remaining 15000 can exist as thirty 500 rupee notes.
Since the total donation amount is 15,250 rupees, there should be at least one 250 rupee note. The remaining 15000 can exist as thirty 500 rupee notes.
| Rs. 250 | Rs. 500 | Rs. 100 | Number of notes |
| 1 | 30 | 0 | 31 |
But the total number of notes will only be 31. We have 100 notes. So to keep the number of 500 notes as high as possible let’s convert the 500 rupee notes to 100 rupee notes. Every time we do this conversion we add 4 new notes.
| Rs. 250 | Rs. 500 | Rs. 100 | Number of notes |
| 1 | 30 | 0 | 31 |
| 1 | 29 | 5 | 35 |
| We add 4 new notes in each conversion, Our target is to reach 100 notes from 35 notes, the closest we can got to 100 by adding only 4’s to 35 is 99 99 = 35 + 4 (16) So this happens after 16 steps |
|||
| 1 | 13 | 85 | 99 |
From here, we can convert one 500 rupee note to two 250 rupee notes.
| 3 | 12 | 85 | 100 |
So, the maximum number of 500 rupee notes is 12
A school has less than 5000 students and if the students are divided equally into teams of either 9 or 10 or 12 or 25 each, exactly 4 are always left out. However, if they are divided into teams of 11 each, no one is left out. The maximum number of teams of 12 each that can be formed out of the students in the school is
Video Explanation

Explanatory Answer
Let the number of students in the school be N.
N < 5000
N leaves a remainder of 4 when divided by 9, 10, 12, or 25.
Since 4 is less than 9, 10, 12 and 25
N leaves a remainder of 4 when divided by LCM(9, 10, 12, 25).
N leaves a remainder of 4 when divided by 900.
N = 900(x) + 4
Since N < 5000
x can range from 0 to 5
But 900(x) + 4 is a multiple of 11 only when x = 2
N = 900(2) + 4 = 1804
When we divide these 1804 students into groups of 12, we get, 150 groups.
Because, 1804 = 12(150) + 4
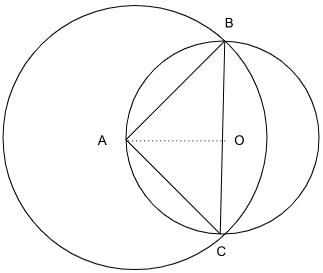
In a triangle ABC, AB = AC = 8cm. A circle drawn with BC as diameter passes through A. Another circle drawn with center at A passes through B and C. Then the area, in sq. cm, of the overlapping region between the two circles is
Video Explanation

Explanatory Answer

The average of all 3-digit terms in the arithmetic progression 38, 55, 72, ., is
Video Explanation

Explanatory Answer

A group of N people worked on a project. They finished 35% of the project by working 7 hours a day for 10 days. Thereafter, 10 people left the group and the remaining people finished the rest of the project in 14 days by working 10 hours a day. Then the value of N is
Video Explanation

Explanatory Answer
N people finish 35% of the project by working 7 hours a day for 10 days.
N people finish 35% of the project by working 70 hours.
N people finish 5% of the project by working 10 hours.
N people finish 65% of the project by working 130 hours.
65% of the project is done in N * 130 man hours.
The remaining 65% was actually done by (N-10) people in 14 days by working 10 hours a day.
(N-10) people finish 65% of the project by working 140 hours.
65% of the project is done in (N - 10) * 140 man hours.
N * 130 = (N - 10) * 140
13N = 14N - 140
N = 140
Consider six distinct natural numbers such that the average of the two smallest numbers is 14, and the average of the two largest numbers is 28. Then, the maximum possible value of the average of these six numbers is
Video Explanation

Explanatory Answer
We know the sum of the first pair of numbers is 14 * 2 = 28
Sum of the last pair of numbers is 28 * 2 = 56
To maximize the average of all the 6 numbers, we must try to maximize the two numbers in between. This is possible when the last pair of numbers are 27 and 29.
The maximum average case is
a, b, 25, 26, 27, 29
Where a + b = 28
The average of these 6 numbers is 22.5
Moody takes 30 seconds to finish riding an escalator if he walks on it at his normal speed in the same direction. He takes 20 seconds to finish riding the escalator if he walks at twice his normal speed in the same direction. If Moody decides to stand still on the escalator, then the time, in seconds, needed to finish riding the escalator is
Video Explanation

Explanatory Answer

Two cars travel from different locations at constant speeds. To meet each other after starting at the same time, they take 1.5 hours if they travel towards each other, but 10.5 hours if they travel in the same direction. If the speed of the slower car is 60 km/hr, then the distance traveled, in km, by the slower car when it meets the other car while traveling towards each other, is
Video Explanation

Explanatory Answer
Let the distance between the 2 cars be D km.
Let the speeds of the two cars be ‘a’ and ‘b’ respectively and a > b.
Case I)
Cars are moving in the opposite direction (towards each other)
Relative speed = a + b
Time taken = 1.5 hrs
Case II)
Cars are moving in the same direction (Car A chasing Car B)
Relative speed = a - b
Time taken = 10.5 hrs
In both the cases the distance between the cars is the same, ‘D’.
But the time taken is in the ratio 1.5 : 10.5 or 1 : 7
Therefore, the speeds will be in the ratio 7 : 1
a + b = 7(a - b)
8b = 6a
3a = 4b
Substituting b = 60 kmph,
We get, a = 80 kmph.
D = (a + b) * 1.5 = 210km
When they move towards each other the distance covered by them is in the ratio 4 : 3 and the total distance covered by them together is 210 km.
The slower car, B, covers 3/7 th of this 210 km which is 90 km.
Nitu has an initial capital of ₹20,000. Out of this, she invests ₹8,000 at 5.5% in bank A, ₹5,000 at 5.6% in bank B and the remaining amount at x% in bank C, each rate being simple interest per annum. Her combined annual interest income from these investments is equal to 5% of the initial capital. If she had invested her entire initial capital in bank C alone, then her annual interest income, in rupees, would have been
Video Explanation

Explanatory Answer
If Neetu intended to get a 5% annual interest, ideally all the banks should have maintained a 5% interest rate.
But Bank A returns 0.5% extra interest on 8000 rupees, which is 40 rupees.
But Bank B returns 0.6% extra interest on 5000 rupees, which is 30 rupees.
A & B combines are paying 70 rupees extra than 5%.
So Bank C should maintain such an interest rate that, the interest generated on the remaining 7000 rupees is 70 less than 5% interest.
Since 70 is 1% of 7000. The interest rate at Bank C should be 5% - 1% = 4%
If all the 20,000 rupees were invested in Bank C, the interest generated is 4% of 20,000 = 800 rupees.
The arithmetic mean of all the distinct numbers that can be obtained by rearranging the digits in 1421, including itself, is
Video Explanation

Explanatory Answer

Suppose the medians BD and CE of a triangle ABC intersect at a point O. If area of triangle ABC is 108 sq. cm., then, the area of the triangle EOD, in sq. cm., is
Video Explanation

Explanatory Answer
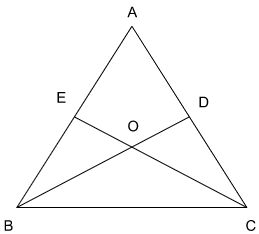
O is the centroid of the triangle ABC,that means,
BO : OD = 2 : 1
CO : OE = 2 : 1
Ar(BOC) : Ar(ODC) = 2 : 1
Ar(COB) : Ar(OEB) = 2 : 1
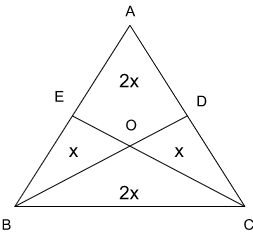
Since BD is the median, Ar(BDA) = Ar(BDC)
This means Ar(AEOD) = 2x
2x + x + x + 2x = 108
6x = 108
Ar(AEOD) = 2x = 36
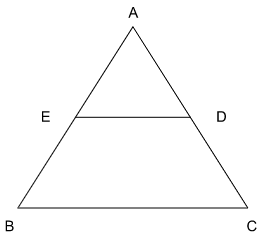
Since ED is the line joining the midpoints of AB and AC, Ar(AED) = ¼ Ar(ABC)
Ar(AED) = ¼ Ar(108) = 27
Ar(EOD) = Ar(AEOD) - Ar(AED) = 36 - 27 = 9 sq cm
In an examination, the average marks of students in sections A and B are 32 and 60, respectively. The number of students in section A is 10 less than that in section B. If the average marks of all the students across both the sections combined is an integer, then the difference between the maximum and minimum possible number of students in section A is
Video Explanation

Explanatory Answer


A glass contains 500 cc of milk and a cup contains 500 cc of water. From the glass, 150 cc of milk is transferred to the cup and mixed thoroughly. Next, 150 cc of this mixture is transferred from the cup to the glass. Now, the amount of water in the glass and the amount of milk in the cup are in the ratio
Video Explanation

Explanatory Answer
Imagine 2 beakers of milk and water each of volume 500 cc
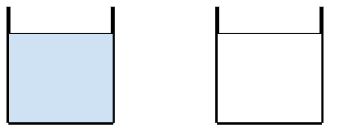
After the transfer of liquids from one beaker to another, both the beakers end up having the same volume of 500 cc again.
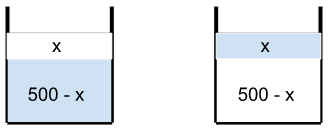
If there is x cc of Milk in the first beaker, there will be 500 - x cc of water in the second beaker, the remaining x cc of water should be in the second beaker!
Therefore, the amount of water in the glass and the amount of milk in the cup are equal and hence in the ratio 1 : 1.
It does not matter how many times the liquids are transferred, if the final volumes are 500 cc, then, the amount of water in the glass and the amount of milk in the cup will be in the ratio 1 : 1.
Bob can finish a job in 40 days, if he works alone. Alex is twice as fast as Bob and thrice as fast as Cole in the same job. Suppose Alex and Bob work together on the first day, Bob and Cole work together on the second day, Cole and Alex work together on the third day, and then, they continue the work by repeating this three-day roster, with Alex and Bob working together on the fourth day, and so on. Then, the total number of days Alex would have worked when the job gets finished, is
Video Explanation

Explanatory Answer
Since Alex is twice as fast as Bob and thrice as fast as Cole, let us assume that the work done by Alex in a day as 6x.
This means that the work done by Bob and Cole in a day is 3x and 2x respectively.
| Alex | Bob | Cole |
| 6x | 3x | 2x |
Since Bob can finish the job in 40 days working alone, the quantum of work to finish the job = 40 ×× 3x = 120x
The work done on the first day, the second day, and the third day is as follows.
| Day 1 (Alex & Bob) |
Day 2 (Bob & Cole) |
Day 3 (Cole & Alex) |
| 9x | 5x | 8x |
The total work done in one cycle of 3 days = 9x + 5x + 8x = 22x
120x = 22x(5) + 9x + 1x
This means, it takes 5 complete cycles of 3 days, a full Day 1 and Day 2 to finish the job.
In one cycle Alex works twice, on Day 1 and Day 3.
So the total number of days that Alex works = 2(5) = 1 = 11 days
Let an and bn be two sequences such that an=13+6(n−1) and bn=15+7(n−1) for all natural numbers n. Then, the largest three digit integer that is common to both these sequences, is
Video Explanation

Explanatory Answer
an=13+6(n−1)=7+6n
bm=15+7(m−1)=8+7m
For some m, n, let 7+6n=8+7m
6n−7m=1
n=6,m=5
a6=43 and b5=43
Since, L.C.M(6,7)=42, the common terms of the series are of the form 43+42k
Let’s find the smallest 4-digit number of this form…
1000/42≅23.80100042≅23.80
43+42(23)=100943+42(23)=1009
∴43+42(22)=967∴43+42(22)=967 is the largest 3-digit such value.
The area of the quadrilateral bounded by the Y-axis, the line X =5, and the lines |x−y|−|x−5|=2, is
Video Explanation

Explanatory Answer
We need to find the area of the quadrilateral ABDE = area of rectangle ABCD + area of triangle
CDE => Area of ABCD = (7-3)*5 = 20 units, and the area of triangle CDE = (1/2)*10*5 = 25
units.
Hence, the area of the quadrilateral ABDE = (20+25) = 45 units
A triangle is drawn with its vertices on the circle C such that one of its sides is a diameter of C and the other two sides have their lengths in the ratio a:b. If the radius of the circle is r, then the area of the triangle is
Video Explanation

Explanatory Answer

In a rectangle ABCD, AB = 9 cm and BC = 6 cm. P and Q are two points on BC such that the areas of the figures ABP, APQ, and AQCD are in geometric progression. If the area of the figure AQCD is four times the area of triangle ABP, then BP : PQ : QC is
Video Explanation

Explanatory Answer
Since Ar(ABP),Ar(APQ)&Ar(AQCD) are in GP and Ar(AQCD)=4×Ar(ABP)
Ar(ABP):Ar(APQ):Ar(AQCD)=1:2:4
9x/2:9y/2:27+9z/2=1:2:4
x:y:6+z=1:2:4
y=2x
6+z=4x
x + y + z = 6
x + 2x + 4x – 6 = 6
x = 127127
z = 4x – 6 = 48−427=6748−427=67
∴ x = 2z
Therefore, x:y:z=2:4:1
BP : PQ : QC = 2 : 4 : 1
If a certain amount of money is divided equally among n persons, each one receives Rs 352 . However, if two persons receive Rs 506 each and the remaining amount is divided equally among the other persons, each of them receive less than or equal to Rs 330 . Then, the maximum possible value of n is
Video Explanation

Explanatory Answer
Let the total amount be equal to T.
T=n×352
“However, if two persons receive Rs 506 each and the remaining amount is divided equally among the other persons, each of them receive less than or equal to Rs 330”
T≤2×506+(n−2)×330
n×352≤2×506+(n−2)×330
n×352≤352+n×330
n×22≤352
n≤352/22
n≤16
So, the maximum value that n can take is 16.
Jayant bought a certain number of white shirts at the rate of Rs 1000 per piece and a certain number of blue shirts at the rate of Rs 1125 per piece. For each shirt, he then set a fixed market price which was 25% higher than the average cost of all the shirts. He sold all the shirts at a discount of 10% and made a total profit of Rs 51000. If he bought both colors of shirts, then the maximum possible total number of shirts that he could have bought is
Video Explanation

Explanatory Answer
Let the number of white and black shirts bought by Jayant be w and b respectively.
Then the total Cost Price (CP) =1000×w+1125×b=1000(w+b)+125×b
Since the goods are marked up by 25% and then offered at a discount of 10%, the total Selling
Price (SP) =CP×1.25×0.9=1.125
This implies that there was a 12.5% of Profit, which is given to be 51, 000
12.5%(CP) = 51,000
CP = 4,08,000
1000(w+b)+125×b=4,08,000
w and b are positive integers (since at least one shirt of each color needs to be purchased.)
To purchase maximum number of shirts, you need to purchase minimum number of the costlier shirts, which are the blue ones
Observe that the total CP is a multiple of 1000. And for that to happen b should be a multiple of 8 in 1000(w+b)+125×b=4,08,000
So the minimum value of b = 8, in which case, w = 399. Hence, the maximum number of shirts
that can be purchased = 399 + 8 = 407
A container has 40 liters of milk. Then, 4 liters are removed from the container and replaced with 4 liters of water. This process of replacing 4 liters of the liquid in the container with an equal volume of water is continued repeatedly. The smallest number of times of doing this process, after which the volume of milk in the container becomes less than that of water, is
Video Explanation

Explanatory Answer

Two ships meet mid-ocean, and then, one ship goes south and the other ship goes west, both travelling at constant speeds. Two hours later, they are 60 km apart. If the speed of one of the ships is 6 km per hour more than the other one, then the speed, in km per hour, of the slower ship is
Video Explanation

Explanatory Answer
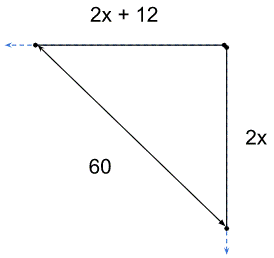
Let the speeds of the boats be x kmph and x + 6 kmph.
After 2 hours, the distance travelled by the boats is 2x km and 2x + 12 kms respectively.
The distance between them is 60 kms.
602 = (2x)2 + (2x + 12)2
3600 = 4 x2 + 4 x2 + 144 + 48x
900 = 2 x2 + 36 + 12 x
450 = x2 + 18 + 6 x
x2 + 6x - 432 = 0
x2 + 24x - 18x - 432 = 0
x = 18 or x = -24
The speed of the slower boat is 18 kmph.
Mr. Pinto invests one-fifth of his capital at 6%, one-third at 10% and the remaining at 1%, each rate being simple interest per annum. Then, the minimum number of years required for the cumulative interest income from these investments to equal or exceed his initial capital is
Video Explanation

Explanatory Answer
Let the capital invested by Mr.Pinto be ₹300.
₹300 because we deal with one-third, further in the question.
| Investments | Invested amount | Rate of interest | Return |
| one-fifth | 60 | 6% | ₹3.6 |
| one-third | 100 | 10% | ₹10 |
| remaining | 140 | 1% | ₹1.4 |
| Total return in a year | ₹15 | ||
The interest generated is ₹15 per year.
Let’s say the capital is invested for n years.
When return equals capital…
15 n = 300
n = 20.
Five students, including Amit, appear for an examination in which possible marks are integers between 0 and 50, both inclusive. The average marks for all the students is 38 and exactly three students got more than 32. If no two students got the same marks and Amit got the least marks among the five students, then the difference between the highest and lowest possible marks of Amit is
Video Explanation

Explanatory Answer
The case where Amit gets the least amount of marks looks like…
The maximum mark that Amit can get is 31, He can get it if he can grab 20 marks from the people who score 48, 49 and 50.
In fact, it is possible for Amit to do that…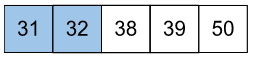
The difference between the highest and lowest marks if Amit = 31 - 11 = 20.
In an examination, there were 75 questions. 3 marks were awarded for each correct answer, 1 mark was deducted for each wrong answer and 1 mark was awarded for each unattempted question. Rayan scored a total of 97 marks in the examination. If the number of unattempted questions was higher than the number of attempted questions, then the maximum number of correct answers that Rayan could have given in the examination is
Video Explanation

Explanatory Answer
The rules of the examination are…
● A correct answer gets +3 marks.
● A wrong answer gets -1 mark.
● An unanswered question gets +1 mark.
So, the scenario is, every question is already awarded 1 mark before attempting, if the attempt is right you get +2 marks and if it is wrong you get -2 marks.
So after re-imagining the examination…
● Every Question is awarded + 1 before attempting itself.
(This means you enter the examination with 75 marks in your pocket)
● A right answer fetches +2 marks.
● A wrong answer fetches -2 marks.
Now it is up to the student to increase or decrease his total marks from 75.
If he answers more questions right than wrong he gets additional marks.
If he answers more questions wrong than right his marks decrease.
So, when Rayan scored a total of 97 marks in the examination, 75 were given to him on a platter. The remaining 22 is what he put effort to score.
This means the difference between the number of questions he got right and the number of questions he got wrong is 11.
In the most extreme case, he might have got 11 questions right and did not attempt the remaining.
| Right | Wrong | Unattempted |
| 11 | 0 | 64 |
He might have got a few questions wrong, but the number of right questions should always be more than the number of wrong questions by 11.
The case where the number of wrong questions is ‘x’ looks like…
| Right | Wrong | Unattempted |
| 11 + x | x | 64 - 2x |
The number of unattempted questions was higher than the number of attempted questions…
This means,
64 - 2x > 11 + x + x
53 > 4x
x≤13x≤13.
The maximum value of x is 13.
The maximum number of the right answers = 11 + 13 = 24
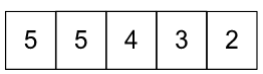
The number of integers greater than 2000 that can be formed with the digits 0, 1, 2, 3, 4, 5, using each digit at most once, is
Video Explanation

Explanatory Answer
The number of 6-digit integers that can be formed is 600.
The number of 5-digit integers that can be formed is 600.
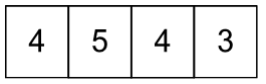
The number of 4-digit integers that can be formed is 240.
The total number of integers greater than 2000 that can be formed with the digits 0, 1, 2, 3, 4, 5,
using each digit at most once, is 600 + 600 + 240 = 1440
In an election, there were four candidates and 80% of the registered voters casted their votes. One of the candidates received 30% of the casted votes while the other three candidates received the remaining casted votes in the proportion 1 : 2 : 3. If the winner of the election received 2512 votes more than the candidate with the second highest votes, then the number of registered voters was
Video Explanation

Explanatory Answer
One candidate got 30% of the polled votes, the remaining three got in the ratio of 1 : 2 : 3
The polled votes were split in 3 : 7 ratio.
The 70% of them were again split in the ratio 1 : 2 : 3
The votes were polled in the ratio of 6(3) : 7(1 : 2 : 3)
18 : 7 : 14 : 21
Let’s assume that the actual polled votes are 18x, 7x, 14x, 21x
The winner of the election received 2512 votes more than the candidate with the second highest votes.
21x - 18x = 2512
3x = 2512
Total polled votes = 18x + 7x + 14x + 21x = 60x = 20(3x) = 20(2512) = 50,240
The polled votes represent 80% of the total registered votes.
Total registered votes = 50,240 + 12,560 = 62,800.
The average of a non-decreasing sequence of N numbers a1,a2,…,aN is 300 . If a1 is replaced by 6a1, the new average becomes 400. Then, the number of possible values of a1 is
Video Explanation

Explanatory Answer
a1 + a2 + a3 + … + an = 300(n)
6a1 + a2 + a3 + … + an = 400(n)
5a1 = 100(n)
a1 = 20(n)
The constraints of the problem are:
● Sum of n terms = 300(n)
● The first term is 20(n)
● All other terms (terms other than the first term) should be greater than or equal to the first term. (Because the sequence is a non-decreasing sequence.)
Image a scenario where all the other terms are equal to the first term. That is a case where all the terms are equal. Since the average is 300. All of them should be 300. The first term is 300.
20(n) = 300
n = 15
Now imagine that the sequence has 16 terms the first term will be 320, and all the other terms will be greater than or equal to 320. So the average can’t be 300.
Or basically, the maximum number of terms in the sequence is 15.
What is the minimum number of terms in the sequence?
Can the sequence have one term?
n = 1
a1 = 20
But the sum of terms is not 300.
The sequence should have more than one term.
n = 2
a1 = 2(20) = 40
The sum of terms can be 300(2). This happens by having the second term as 560.
The minimum number of terms in the sequence is 2.
The maximum number of terms in the sequence is 15.
The number of terms in the sequence can have 14 different values.
And in each case the value of a1 is distinct.
Hence, a1 can have 14 different values.
On day one, there are 100 particles in a laboratory experiment. On day n, where n≥2, one out of every n particles produces another particle. If the total number of particles in the laboratory experiment increases to 1000 on day m, then m equals
Video Explanation

Explanatory Answer

There are two containers of the same volume, first container half-filled with sugar syrup and the second container half-filled with milk. Half the content of the first container is transferred to the second container, and then the half of this mixture is transferred back to the first container. Next, half the content of the first container is transferred back to the second container. Then the ratio of sugar syrup and milk in the second container is
Video Explanation

Explanatory Answer
Let the half volume of each container be 80 cc.
Why 80cc though? Why not some other value?
We know that the process of shifting half volumes is happening three times overall.
(12)3=18(12)3=18.
So it would be wise to assume the initial volume to be some multiple of 8 so that we don’t have to deal with fractions later on.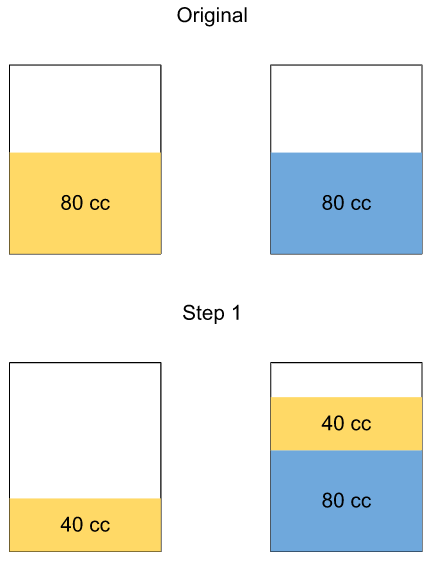
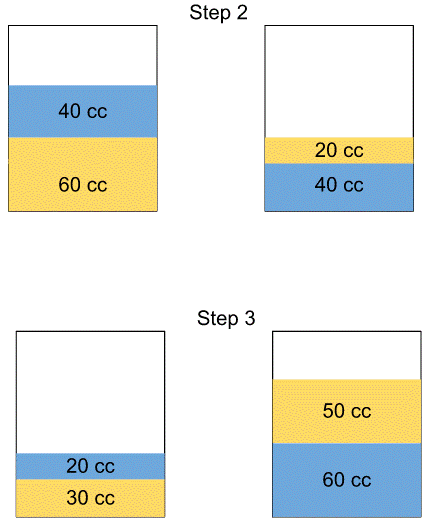
The ratio of Sugar Syrup to Water in the second container is 5 : 6.
Manu earns ₹4000 per month and wants to save an average of ₹550 per month in a year. In the first nine months, his monthly expense was ₹3500, and he foresees that, tenth month onward, his monthly expense will increase to ₹3700. In order to meet his yearly savings target, his monthly earnings, in rupees, from the tenth month onward should be
Video Explanation

Explanatory Answer
On average, Manu targets saving ₹550 per month.
In the first 9 months, Manu earns ₹4000 per month and spends ₹3500.
So, he ends up saving only ₹450 per month. In other words, he misses his target by ₹50 per month.
So he saves ₹50 ×× 9 = ₹450 less than his target.
In the next 3 months of the year, his expenses are ₹3700 per month. To save ₹550 per month in these three months, his income should be ₹3700 + ₹550 = ₹4250 per month.
But also, he should earn some more to compensate for the ₹450 he was short of in the first 9 months. This ₹450 is earned over a span of 3 months. Or he should earn ₹150 extra each month.
So Manu’s income in the last 3 months = ₹4250 + ₹150 = ₹4400