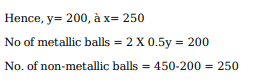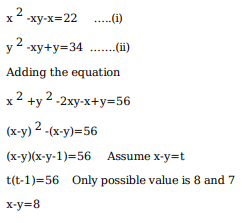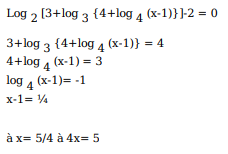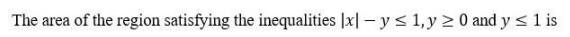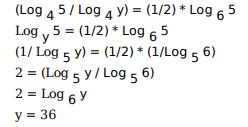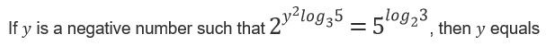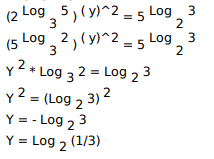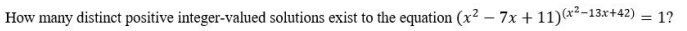Live Updates
• CATKing has launched new chat bot.

• New video on Logs has been released.
495
Learners
asked the doubt

Previous Year Questions
Three positive integers x, y and z are in arithmetic progression. If y − x > 2 and xyz = 5(x + y + z), then z − x equals
Video Explanation

Explanatory Answer
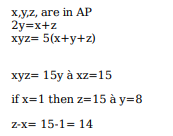
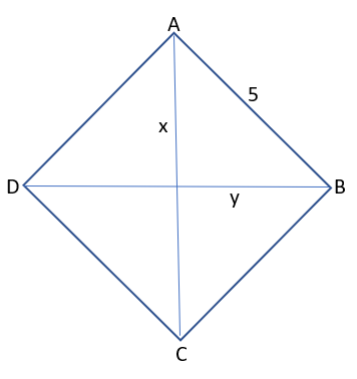
If a rhombus has area 12 sq cm and side length 5 cm, then the length, in cm, of its longer diagonal is
Video Explanation

Explanatory Answer

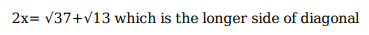
Anil, Bobby and Chintu jointly invest in a business and agree to share the overall profit in proportion to their investments. Anil's share of investment is 70%. His share of profit decreases by ₹ 420 if the overall profit goes down from 18% to 15%. Chintu's share of profit increases by ₹ 80 if the overall profit goes up from 15% to 17%. The amount, in INR, invested by Bobby is
Video Explanation

Explanatory Answer

Anil can paint a house in 60 days while Bimal can paint it in 84 days. Anil starts painting and after 10 days, Bimal and Charu join him. Together, they complete the painting in 14 more days. If they are paid a total of ₹ 21000 for the job, then the share of Charu, in INR, proportionate to the work done by him, is
Video Explanation

Explanatory Answer
Let’s assume total work to be 420 units
Anil = 420/60 = 7 units/day
Bimal = 420/84 = 5 units /day
After 10 days, total work left = 420 -70 = 350
Now to do 350 units of work in 14 days, has to work 25 unit per day
C’s work= 25-7-5= 13 units a day
In term of work A B C
168 70 182
Profit of C = 182/420 * 21000 = 9100
Two trains A and B were moving in opposite directions, their speeds being in the ratio 5 : 3. The front end of A crossed the rear end of B 46 seconds after the front ends of the trains had crossed each other. It took another 69 seconds for the rear ends of the trains to cross each other. The ratio of length of train A to that of train B is
Video Explanation

Explanatory Answer

From a container filled with milk, 9 litres of milk are drawn and replaced with water. Next, from the same container, 9 litres are drawn and again replaced with water. If the volumes of milk and water in the container are now in the ratio of 16 : 9, then the capacity of the container, in litres, is
Video Explanation

Explanatory Answer
Let the initial quantity (Capacity of Container) = x
Milk / Total = 16/25 = [(x -9)/x] 2=> 4/5 = (x - 9)/x=> x = 45
The number of ways of distributing 15 identical balloons, 6 identical pencils and 3 identical erasers among 3 children, such that each child gets at least four balloons and one pencil, is
Video Explanation

Explanatory Answer
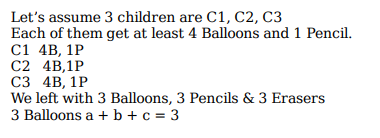

A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is
Video Explanation

Explanatory Answer
Height of Cone = 27 cm
The Larger cone after passing a plane has a smaller cone with height 9 cm (27-18)
The heights are in the ratio 9 : 27 or 1 : 3
Volumes will be in ratio of (Height) 3
Volume of smaller cone : Volume of whole cone à 1 : 27
Volume of remaining cone = 27x – 1x = 26x
26x – x = 225cc
x = 9cc
Volume of original cone = 27*9 = 243 cc
If a, b and c are positive integers such that ab = 432, bc = 96 and c < 9, then the smallest possible value of a + b + c is
Video Explanation

Explanatory Answer
We need the sum of a+b+c to be minimum hence the values of a,b ,c must be as close as
possible
ab = 432 = 18*24
bc = 96 = 24*4
a + b + c = 18 + 24 + 4 = 46
A train travelled at one-thirds of its usual speed, and hence reached the destination 30 minutes after the scheduled time. On its return journey, the train initially travelled at its usual speed for 5 minutes but then stopped for 4 minutes for an emergency. The percentage by which the train must now increase its usual speed so as to reach the destination at the scheduled time, is nearest to
Video Explanation

Explanatory Answer
Original speed = S & Original time = T
New Speed = S/3, speed and time are inversely proportional hence New time = 3T
The difference between times = 3T-T = 30 mins
Original time taken = 15 mins
Assume Distance is 15 Kms and Speed = 1 km/hr
In 5 mins the train travelled 5 kms and 4 mins it stopped.
In 6 mins it has to cover 10 kms
The original speed will be increased by a factor of 1.66 or 67%
If f(5 + x) = f(5 – x) for every real x, and f (x) = 0 has four distinct real roots, then the sum of these roots is
Video Explanation

Explanatory Answer
As f(x) = 0 we must try to convert f(5+x) = f(5-x) in terms of f(x)
We substitute x as x-5
f(x) = f(10-x)
Lets assume x = A as a root, then we simultaneously get 10-A as a root
Similarly we assume x = B as a root, then we get 10-B as a root
the 4 roots are A, B, 10-A, 10-B
The sum of roots is 20
Veeru invested Rs 10000 at 5% simple annual interest, and exactly after two years, Joy invested Rs 8000 at 10% simple annual interest. How many years after Veeru’s investment, will their balances, i.e., principal plus accumulated interest, be equal?
Video Explanation

Explanatory Answer
2 years simple interest accrued by Veeru is Rs. 1000
10000 + 1000 + 10000*0.05*x = 8000 + 8000*0.1*x
3000 = 300x
x = 10 years
2 years of Veeru’s initial investment hence answer = 10+2 = 12 years
Let A, B and C be three positive integers such that the sum of A and the mean of B and C is 5. In addition, the sum of B and the mean of A and C is 7. Then the sum of A and B is
Video Explanation

Explanatory Answer
A + (B+C)/2 = 5 à 2A + B + C = 10 - Eq 1
B + (A+C)/2 = 7 à A + 2B + C = 14 - Eq 2
Subtracting, Eq2 – Eq1
B = 4 + A
Adding Eq 1 and Eq 2
3(A+B) + 2C = 24 – Eq 3
Now since A B C are positive and B = 4 + A hence A+B cannot be equal to 4
In Eq 3 all components have to be even thereby eliminating 5 and 7.
Hence A+B = 6.
Two persons are walking beside a railway track at respective speeds of 2 and 4 km per hour in the same direction. A train came from behind them and crossed them in 90 and 100 seconds, respectively. The time, in seconds, taken by the train to cross an electric post is nearest to
Video Explanation

Explanatory Answer
Assume length of Train as L and Original speed as S
To cross the first person (2 kmph) train needs 90 seconds at S-2 km/hr and to cross the second
person (2 kmph) train needs 100 seconds at S-4 km/hr
Speeds are inversely proportional to time
(S-2)/(S-4) = (100/90)
S = 22
(S-2) = L * 3600 / 90
L = 0.5 km
T = (0.5 * 3600) / 22 = 82 seconds
A straight road connects points A and B. Car 1 travels from A to B and Car 2 travels from B to A, both leaving at the same time. After meeting each other, they take 45 minutes and 20 minutes, respectively, to complete their journeys. If Car 1 travels at the speed of 60 km/hr, then the speed of Car 2, in km/hr, is
Video Explanation

Explanatory Answer
A person spent Rs 50000 to purchase a desktop computer and a laptop computer. He sold the desktop at 20% profit and the laptop at 10% loss. If overall he made a 2% profit then the purchase price, in rupees, of the desktop is
Video Explanation

Explanatory Answer
Cost of Desktop = D
Cost of Laptop = L
D + L = 50000 à Eq 1
1.2*D + 0.9*L = 51000 à Eq 2
Multiplying Eq 1 by 0.9 and subtracting with Eq 2
0.3*D = 6000
D = Rs. 20000
On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is:
Video Explanation

Explanatory Answer

A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is:
Video Explanation

Explanatory Answer
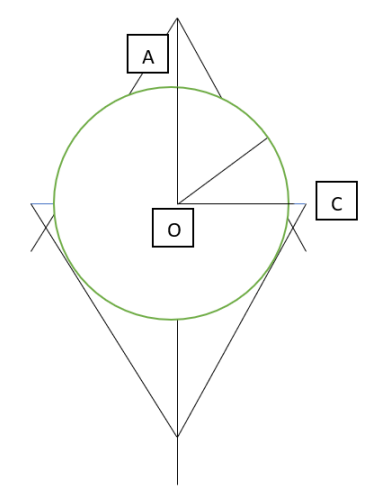
AOC is a right-angle triangle and AC = 10
Perpendicular of a right-angle triangle = P*B/H = 8*6 / 10 = 4.8
Area of circle = P *4.8*4.8 / (0.5*12*16) = 6* P / 25
A gentleman decided to treat a few children in the following manner. He gives half of his total stock of toffees and one extra to the first child, and then the half of the remaining stock along with one extra to the second and continues giving away in this fashion. His total stock exhausts after he takes care of 5 children. How many toffees were there in his stock initially?
Video Explanation

Explanatory Answer
These questions work with a backward approach.
The 5 child gets half of what was remaining after 4 child + 1, this essentially means the 5 child
got 2 toffees.
Now the gentleman had 2 toffees after giving half of what was remaining after child 3 + 1, this
means he had 2*(2+1) = 6 left after giving the third child. Hence the 4-child got
0.5*6 + 1 = 4 and 2 were left for 5-child.
Similarly, after giving second child he had 2*(6+1) = 14 toffees
After giving first child he had 2*(14+1) = 30 toffees
Initially he had 2*(30+1) = 62 toffees
The mean of all 4 digit even natural numbers of the form 'aabb', where a>0, is
Video Explanation

Explanatory Answer
The even numbers will be of the form
1100, 1122, 1144, 1166, 1188
2200, 2222, 2244, 2266, 2288 and so on
There will be 45 such numbers from 1100 to 9988, the mean will be the 23 number which is 5544
An alloy is prepared by mixing three metals A, B and C in the proportion 3:4:7 by volume. Weights of the same volume of the metals A, B and C are in the ratio 5:2:6. In 130 kg of the alloy, the weight, in kg, of the metal C is:
Video Explanation

Explanatory Answer
We have been given the ratio of the volume and weights of the volume (1-unit cube of A will
have a weight of 5x).
Hence to find the actual weights we must multiply the volume and weights of volume.
A : B : C = (3*5 : 4*2 : 7*6) = 15 : 8 : 42
Total weight = 15x + 8x + 42x = 65x = 130
x = 2
Therefore weight of C = 42*2 = 84 Kgs
A solution, of volume 40 litres, has dye and water in the proportion 2 : 3. Water is added to the solution to change this proportion to 2 : 5. If one-fourths of this diluted solution is taken out, how many litres of dye must be added to the remaining solution to bring the proportion back to 2 : 3?
Video Explanation

Explanatory Answer
Solution = 40 litres
Dye = 16 litres
Water = 24 litres
New amount of water in the solution will be 5*8 = 40 litres, i.e 16 litres of water has been added
Solution = 56 litres
We remove ¼ or 14 litres, which leaves 42 litres with dye = 12 litres and water = 30 litres
We need 8 litres of dye to get the proportion to 2:3
In a group of people, 28% of the members are young while the rest are old. If 65% of the members are literates, and 25% of the literates are young, then the percentage of old people among the illiterates is nearest to
Video Explanation

Explanatory Answer
Let’s Assume there are 400 people
Young – 112
Old – 288
Illiterates = 140
Literates = 260
Young literate = 65
Old Literates = 195
Old illiterates = 93
Old illiterates / Total illiterates = 93/140 = 66%
How many 3-digit numbers are there, for which the product of their digits is more than 2 but less than 7?
Video Explanation

Explanatory Answer
Let’s start with numbers with products 3 4 5 6
113, 131, 311
122, 212, 221
114, 141, 411
115, 151, 511
123, 132, 213, 312, 231, 321
116, 161, 611
21 Solutions
Leaving home at the same time, Amal reaches office at 10:15 am if he travels at 8 km/hr, and at 9:40 am if he travels at 15 km/hr. Leaving home at 9:10 am, at what speed, in km/hr, must he travel so as to reach office exactly at 10 am?
Video Explanation

Explanatory Answer
At 8 km/hr Amal reaches at 10:15 am and at 15km/hr Amal reaches at 9:40 am.
Lets assume the original time takes as T mins and at 15km/hr the time taken would be T-35 mins
Ratio of speeds is inverse of ratio of time.
(8/15) = (T-35/T)
T = 75 mins
Distance = 8 * (75/60) = 10 kms
Time = (50/60) hr
Speed = 10 * (50/60) = 12 km/hr
The natural numbers are divided into groups as (1), (2, 3, 4), (5, 6, 7, 8, 9), … and so on. Then, the sum of the numbers in the 15th group is equal to
Video Explanation

Explanatory Answer
The natural numbers are divided into groups as (1), (2, 3, 4), (5, 6, 7, 8, 9), ….. and so on.
If you observe that the first group ends with 12, the second group ends with 22and the third group ends with 32
Hence, the 15th group ends with 152 = 225.
The 14th group ends with 142 = 196.
Therefore, the 15th group contains (197, 198, . . . . . . . . . . ,225)
![]()
Amar, Akbar and Anthony are working on a project. Working together Amar and Akbar can complete the project in 1 year, Akbar and Anthony can complete in 16 months, Anthony and Amar can complete in 2 years. If the person who is neither the fastest nor the slowest works alone, the time in months he will take to complete the project is
Video Explanation

Explanatory Answer

The number of groups of three or more distinct numbers that can be chosen from 1, 2, 3, 4, 5, 6, 7 and 8 so that the groups always include 3 and 5, while 7 and 8 are never included together is(assume each number can only occur once)
Video Explanation

Explanatory Answer
Given that the numbers 3 and 5 should be present in every subset and contain at least 3 numbers in it.
First, we need to find the subsets possible
{3, 5, 1, 2, 4, 6, 7, 8} except 3 and 5, remaining all numbers have two possible outcomes that either it is in the set or out of the set.
So, the number of possible subsets containing at least 3 numbers is 26-1 = 63
(In this 26, we have a possibility that nothing is present from {1, 2, 4, 6, 7, 8}. So, we should remove that possibility.)
From these 63, we need to remove the subsets which have {3, 5, 7, 8}
{3, 5, 7, 8, 1, 2, 4, 6} except 3, 5, 7, 8 remaining all numbers {1, 2, 4, 6} have two possible outcomes that either it is in the set or out of the set.
So, the number of sets possible is 24 = 16
Therefore, the answer would be 63 - 16 = 47.
How many three-digit numbers are greater than 100 and increase by 198 when the three digits are arranged in the reverse order?
Video Explanation

Explanatory Answer
Let's consider a three-digit number to be ‘abc’.
Given that, three-digit numbers increase by 198 when the three digits are arranged in the reverse order.
100c + 10b + a - 100a - 10b - c = 198
99c - 99a = 198
c - a = 2
So, the difference between the hundreds place digit and the units place digit is 2.
The possible combinations are:
1 _ 3, 2 _ 4, 3 _ 5, 4 _ 6, 5 _ 7, 6 _ 8, 7 _ 9.
We have 10 numbers for each combination.
Hence, the total numbers are 70.
A circle of diameter 8 inches is inscribed in a triangle ABC where ∠ ABC= 90 °. If BC = 10 inches then the area of the triangle in square inches is
Video Explanation

Explanatory Answer
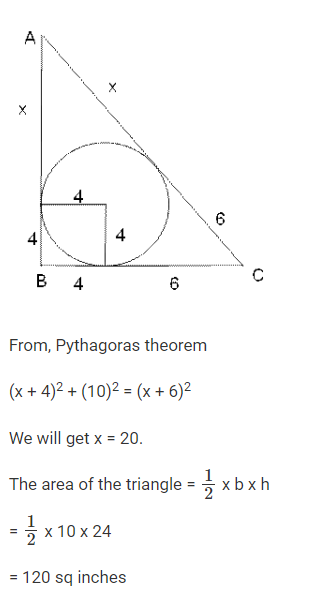
Onion is sold for 5 consecutive months at the rate of Rs 10, 20, 25, 25, and 50 per kg, respectively. A family spends a fixed amount of money on onion for each of the first three months, and then spends half that amount on onion for each of the next two months. The average expense for onion, in rupees per kg, for the family over these 5 months is closest to
Video Explanation

Explanatory Answer
Given that onion is sold for 5 consecutive months at the rate of Rs 10, 20, 25, 25, and 50 per kg respectively.
Let’s consider the amount spend on onions in these five months to be 100, 100, 100, 50, 50.
Hence, the number of kgs in these five months should be 10, 5, 4, 2, 1 respectively.
The average expense on onions per kg over these five months is given by

Therefore, the closest average would be 18.
Two trains cross each other in 14 seconds when running in opposite directions along parallel tracks. The faster train is 160 m long and crosses a lamp post in 12 seconds. If the speed of the other train is 6 km/hr less than the faster one, its length, in m, is
Video Explanation

Explanatory Answer
Speed of faster train = 160/12 m/s
Let's convert it to km/hr = (160/12) x (18/5) = 48 km/hr
Speed of slower train = 48-6= 42 kmph
Trains are moving in opposite directions we must add the speeds and convert to m/s 48+42 =
90x5/18 = 25m/s
(160+x)/14 =25 160 + x = 350
x = 190m
![]()
Video Explanation

Explanatory Answer
|x2 - 4x - 13| = r has exactly three distinct real roots.
Let's complete the squares of the quadratic equation.
|(x - 2)2 - 17| = r
(x - 2)2 - 17 = r and (x - 2)2 - 17 = -r
(x - 2)2 = r + 17 and (x - 2)2 = -r + 17
Hence, we get exactly three roots when r = 17.
The answer is 17.
Amal purchases some pens at ₹ 8 each. To sell these, he hires an employee at a fixed wage. He sells 100 of these pens at ₹ 12 each. If the remaining pens are sold at ₹ 11 each, then he makes a net profit of ₹ 300, while he makes a net loss of ₹ 300 if the remaining pens are sold at ₹ 9 each. The wage of the employee, in INR, is
Video Explanation

Explanatory Answer
Let’s consider the total number of pens to be
(100 +x)
Let's consider the fixed-wage of the labour to be ‘w’
case (i): the net profit is 300
CP = 8(100 +x) + w
SP = 12 x 100 + 11 x = 1200 + 11x
Profit = SP - CP
300 = 1200 + 11x - 8(100 +x) - w
w - 3x = 100 → eq(1)
Case (ii): the net loss is 300
CP = 8(100 +x) + w
SP = 12 x 100 + 9 x = 1200 + 9x
Loss = CP - SP
300 = 8(100 +x) + w - 1200 - 9x
w - x = 700 → eq(2)
By solving equation (1) & (2) we get w = 1000.
Therefore, the wage of the employee is 1000.
Alternate solution:
We can also do this with a little intuition. The Rs 2 decrease per pen results in 300 loss from the case of 300 profit.
The net value of 600 resulted by selling the remaining pens at Rs 2 lesser.
If the number of remaining pens is x, then 2x = 600
So, x = 300.
Total pens = 100 + 300 = 400.
We can get the wage of an employee(w) by considering profit/loss
Profit = 300
100(12) + 300(11) - 400(8) -w = 300
w = 1000
Suppose the length of each side of a regular hexagon ABCDEF is 2 cm. If T is the midpoint of CD, then the length of AT, in cm, is
Video Explanation

Explanatory Answer
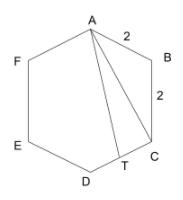
In a regular hexagon, each internal angle is equal to 120°.
From isosceles triangle ABC, we know the length of two sides and including angle.
We will be able to find the third side (AC) using the Pythagoras theorem or the sine rule.
Hence, AC = 2√3cm
Given that, T is the midpoint.
So, CT = 1cm.
From the right-angled △ ACT,
AC2 + CT2 = AT2
AT2 = (2 √3)2 + (1)2 = 13
AT = √(13)
Suppose hospital A admitted 21 less Covid infected patients than hospital B, and all eventually recovered. The sum of recovery days for patients in hospitals A and B were 200 and 152, respectively. If the average recovery days for patients admitted in hospital A was 3 more than the average in hospital B then the number admitted in hospital A was
Video Explanation

Explanatory Answer
Let's consider the number of patients admitted in hospital A and hospital B to be 'x' and ‘x + 21'
Given that, the sum of recovery days for patients in hospitals A and B were 200 and 152, respectively.
The average recovery days for patients admitted in hospital A was 3 more than the average in-hospital B.
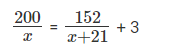
By solving the above equation we get x = 35.
Hence, the number of patients admitted to hospital A is 35.
Anu, Vinu and Manu can complete a work alone in 15 days, 12 days and 20 days, respectively. Vinu works everyday. Anu works only on alternate days starting from the first day while Manu works only on alternate days starting from the second day. Then, the number of days needed to complete the work is
Video Explanation

Explanatory Answer